Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

VDC Toan 2023

Tính tổng các nghiệm của phương trình \({2021^{2021x}} + {2021^{x + 1}}.x = {2021^{{x^2}}} + {2021^x}.{x^2}\).

Ngày Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:, ,

Tính tổng các nghiệm của phương trình \({2021^{2021x}} + {2021^{x + 1}}.x = {2021^{{x^2}}} + {2021^x}.{x^2}\). A. \(2.\) B. \(2021.\) C. \(2022.\) D. \(2023.\) Lời giải Điều kiện: \(x \in \mathbb{R}\) Chia 2 vế của phương trình cho \({2021^x} > 0\), ta được: \({2021^{2020x}} + 2021x = {2021^{{x^2} - x}} + {x^2}\) … [Đọc thêm...] vềTính tổng các nghiệm của phương trình \({2021^{2021x}} + {2021^{x + 1}}.x = {2021^{{x^2}}} + {2021^x}.{x^2}\).

Xét các số thực dương x, y thỏa mãn \({\log _2}\left( {\dfrac{{4x + 2y}}{{2{x^2} + {y^2}}}} \right) \ge 2\left( {{x^2} – x + 1} \right) + \left( {{y^2} – y – 1} \right)\). Tìm giá trị lớn nhất của biểu thức P = x – y + 3xy.

Ngày Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:,

Xét các số thực dương x, y thỏa mãn \({\log _2}\left( {\dfrac{{4x + 2y}}{{2{x^2} + {y^2}}}} \right) \ge 2\left( {{x^2} - x + 1} \right) + \left( {{y^2} - y - 1} \right)\). Tìm giá trị lớn nhất của biểu thức P = x – y + 3xy. A. 3 B. 4 C. 2 D. 0 Giải chi tiết: \(\begin{array}{l}{\log _2}\left( {\dfrac{{4x + 2y}}{{2{x^2} + {y^2}}}} \right) \ge 2\left( {{x^2} - x + 1} \right) + … [Đọc thêm...] vềXét các số thực dương x, y thỏa mãn \({\log _2}\left( {\dfrac{{4x + 2y}}{{2{x^2} + {y^2}}}} \right) \ge 2\left( {{x^2} – x + 1} \right) + \left( {{y^2} – y – 1} \right)\). Tìm giá trị lớn nhất của biểu thức P = x – y + 3xy.

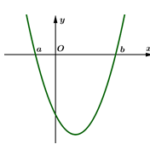
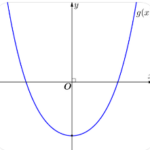
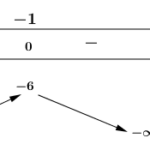
Cho hàm số bậc ba y=f(x) có đồ thị của hàm đạo hàm f'(x) như hình vẽ và f(b)=1. Số giá trị nguyên của \(m \in [-5;5]\) để hàm số \(g\left(x\right)=\left|f^2\left(x\right)+4f\left(x\right)+m\right|\) có đúng 5 điểm cực trị là

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:,

Cho hàm số bậc ba y=f(x) có đồ thị của hàm đạo hàm f'(x) như hình vẽ và f(b)=1. Số giá trị nguyên của \(m\in[-5;5]\) để hàm số \(g\left(x\right)=\left|f^2\left(x\right)+4f\left(x\right)+m\right|\) có đúng 5 điểm cực trị là A. \(8\). B. \(10\). C. \(9\). D. \(7\). LỜI GIẢI Theo bài ra ta có bảng biến thiên của hàm số \(y = f\left( x \right)\) như sau: Đặt … [Đọc thêm...] vềCho hàm số bậc ba y=f(x) có đồ thị của hàm đạo hàm f'(x) như hình vẽ và f(b)=1. Số giá trị nguyên của \(m \in [-5;5]\) để hàm số \(g\left(x\right)=\left|f^2\left(x\right)+4f\left(x\right)+m\right|\) có đúng 5 điểm cực trị là

Có bao nhiêu số nguyên \(x\), \(x \in \left[ { – 10;10} \right]\) thỏa mãn \({3.3^x} + 2x + 1 + \cos 2y = {3^{{{\sin }^2}y}}\)?

Ngày Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình mũ Tag với:,

Có bao nhiêu số nguyên \(x\), \(x \in \left[ { - 10;10} \right]\) thỏa mãn \({3.3^x} + 2x + 1 + \cos 2y = {3^{{{\sin }^2}y}}\)? A. \(2\). B. \(3\). C. \(1\). D. \(0\). Lời giải Ta có: \({3.3^x} + 2x + 1 + \cos 2y = {3^{{{\sin }^2}y}}\) \( \Leftrightarrow {3.3^x} + 2x + 1 + 1 - 2{\sin ^2}y = {3^{{{\sin }^2}y}}\)\( \Leftrightarrow {3^{x + 1}} + 2\left( {x + 1} \right) = … [Đọc thêm...] vềCó bao nhiêu số nguyên \(x\), \(x \in \left[ { – 10;10} \right]\) thỏa mãn \({3.3^x} + 2x + 1 + \cos 2y = {3^{{{\sin }^2}y}}\)?

Có bao nhiêu cặp số nguyên \(\left( {x\,;\,y} \right)\) thỏa mãn \(1 \le x \le 2022\) và \(x + {x^2} – {25^y} = {5^y}\).

Ngày Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình mũ Tag với:, ,

Có bao nhiêu cặp số nguyên \(\left( {x\,;\,y} \right)\) thỏa mãn \(1 \le x \le 2022\) và \(x + {x^2} - {25^y} = {5^y}\). A. \(1010\). B. \(2022\). C. \(7\). D. \(5\). Lời giải Theo bài: \(x + {x^2} - {25^y} = {5^y} \Leftrightarrow x + {x^2} = {5^y} + {25^y}\). Xét hàm \(f\left( t \right) = t + {t^2},\,\,(t > 0)\). Ta có: \(f'\left( t \right) = 1 + 2t > 0,\forall t … [Đọc thêm...] vềCó bao nhiêu cặp số nguyên \(\left( {x\,;\,y} \right)\) thỏa mãn \(1 \le x \le 2022\) và \(x + {x^2} – {25^y} = {5^y}\).

Gọi \(S\) là tập hợp các giá trị thực của tham số \(m\) để hàm số \(y = \frac{1}{3}{x^3} – \frac{1}{2}m{x^2} + 2mx – 5m + 1\) nghịch biến trên một đoạn có độ dài bằng \(3\). Tính tổng tất cả các phần tử của \(S\).

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:,

Gọi \(S\) là tập hợp các giá trị thực của tham số \(m\) để hàm số \(y = \frac{1}{3}{x^3} - \frac{1}{2}m{x^2} + 2mx - 5m + 1\) nghịch biến trên một đoạn có độ dài bằng \(3\). Tính tổng tất cả các phần tử của \(S\). A. \(17\).                        B.  \(8\).                       C.   \(13\).                    D.   \(9\). Lời giải Ta có \(y' … [Đọc thêm...] vềGọi \(S\) là tập hợp các giá trị thực của tham số \(m\) để hàm số \(y = \frac{1}{3}{x^3} – \frac{1}{2}m{x^2} + 2mx – 5m + 1\) nghịch biến trên một đoạn có độ dài bằng \(3\). Tính tổng tất cả các phần tử của \(S\).

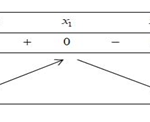
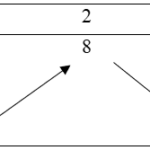
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0\,;\,5} \right]\) và có bảng biến thiên như hình vẽ dưới đây Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt {3x} + \sqrt {10 – 2x} = m\sqrt {f\left( x \right)} \) có nghiệm trên đoạn \(\left[ {0\,;\,5} \right]\)?

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:, ,

Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0\,;\,5} \right]\) và có bảng biến thiên như hình vẽ dưới đây Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt {3x}  + \sqrt {10 - 2x}  = m\sqrt {f\left( x \right)} \) có nghiệm trên đoạn \(\left[ {0\,;\,5} \right]\)? A . 4. B. 7.                              C.   6 . … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0\,;\,5} \right]\) và có bảng biến thiên như hình vẽ dưới đây Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt {3x} + \sqrt {10 – 2x} = m\sqrt {f\left( x \right)} \) có nghiệm trên đoạn \(\left[ {0\,;\,5} \right]\)?

Đề toán 2022 [Mức độ 3] Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = \left| {{x^4} – 2m{x^2} + 64x} \right|\) có đúng ba điểm cực trị?

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:,

Đề toán 2022 [Mức độ 3] Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = \left| {{x^4} - 2m{x^2} + 64x} \right|\) có đúng ba điểm cực trị? A. \(5\). B. \(6\). C. \(12\). D. \(11\). Lời giải Xét hàm số \(g\left( x \right) = {x^4} - 2m{x^2} + 64x\); \(\mathop {\lim }\limits_{x \to  \pm \infty } g\left( x \right) =  + \infty \) \(g\left( x … [Đọc thêm...] về

Đề toán 2022 [Mức độ 3] Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = \left| {{x^4} – 2m{x^2} + 64x} \right|\) có đúng ba điểm cực trị?

Đề toán 2022 [2D1-2.7-4] Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + 2a{x^2} + 8x} \right|\) có đúng ba điểm cực trị.

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:, ,

Đề toán 2022 [2D1-2.7-4] Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + 2a{x^2} + 8x} \right|\) có đúng ba điểm cực trị. A. \(2\). B. \(6\). C.\(5\). D. \(3\). Lời giải Xét hàm số \(g\left( x \right) = {x^4} + 2a{x^2} + 8x\); \(\mathop {\lim }\limits_{x \to  \pm \infty } \,g\left( x \right) =  + \infty \). \(g\left( x … [Đọc thêm...] về

Đề toán 2022 [2D1-2.7-4] Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + 2a{x^2} + 8x} \right|\) có đúng ba điểm cực trị.

Đề toán 2022 Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + a.{x^2} – 8x} \right|\) có đúng ba điểm cực trị?

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:,

Đề toán 2022 Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + a.{x^2} - 8x} \right|\) có đúng ba điểm cực trị? A. \(5\). B. \(6\). C. \(11\). D. \(10\). Lời giải Đặt \(f\left( x \right) = {x^4} + a{x^2} - 8x \Rightarrow f'(x) = 4{x^3} + 2ax - 8.\) \(f'(x) = 0 \Leftrightarrow 4{x^3} + 2ax - 8 = 0 \Leftrightarrow a = \frac{{4 - … [Đọc thêm...] về

Đề toán 2022 Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + a.{x^2} – 8x} \right|\) có đúng ba điểm cực trị?