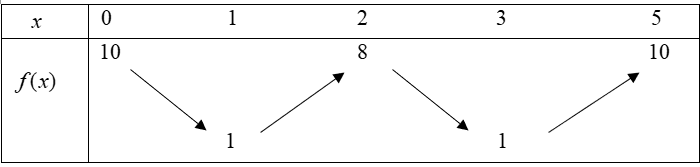
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0\,;\,5} \right]\) và có bảng biến thiên như hình vẽ dưới đây Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt {3x} + \sqrt {10 – 2x} = m\sqrt {f\left( x \right)} \) có nghiệm trên đoạn \(\left[ {0\,;\,5} \right]\)?

Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0\,;\,5} \right]\) và có bảng biến thiên như hình vẽ dưới đây

Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt {3x}  + \sqrt {10 – 2x}  = m\sqrt {f\left( x \right)} \) có nghiệm trên đoạn \(\left[ {0\,;\,5} \right]\)?

A. 4.

B. 7.                            

C.  6.                            

D.  5.

Lời giải

Từ bảng biến biến hàm số \(f\left( x \right)\) suy ra \(\mathop {\max }\limits_{[0\,;\,5]} f\left( x \right) = 10\) tại \(x = 0,x = 5\) và \(\mathop {\min }\limits_{[0\,;\,5]} f\left( x \right) = 1\) tại \(x = 1,\,x = 3\).

Ta có phương trình \(\sqrt {3x}  + \sqrt {10 – 2x}  = m\sqrt {f\left( x \right)}  \Leftrightarrow m = \frac{{\sqrt {3x}  + \sqrt {10 – 2x} }}{{\sqrt {f\left( x \right)} }} = \frac{{h\left( x \right)}}{{\sqrt {f\left( x \right)} }}\)

Xét hàm số \(h\left( x \right) = \sqrt {3x}  + \sqrt {10 – 2x} ,\;x \in [0;5]\)

Có \(h’\left( x \right) = \frac{3}{{2\sqrt {3x} }} – \frac{1}{{\sqrt {10 – 2x} }}\).

\(h’\left( x \right) = 0\)\( \Leftrightarrow \frac{3}{{2\sqrt {3x} }} = \frac{1}{{\sqrt {10 – 2x} }}\)\( \Leftrightarrow 3\sqrt {10 – 2x}  = 2\sqrt {3x} \)\( \Leftrightarrow x = 3\).

Ta có: \(h\left( 0 \right) = \sqrt {10} \),\(h\left( 3 \right) = 5\) và \(h\left( 5 \right) = \sqrt {15} \) nên suy ra:

\(\mathop {\max }\limits_{[0;5]} h\left( x \right) = 5\) tại \(x = 3\) và \(\mathop {\min }\limits_{[0;5]} h\left( x \right) = \sqrt {10} \) tại \(x = 0\).

Xét hàm số \(g\left( x \right) = \frac{{h\left( x \right)}}{{\sqrt {f\left( x \right)} }}\) trên đoạn \(\left[ {0\,;\,5} \right]\). Do \(h\left( x \right) > 0,\,f\left( x \right) > 0,\;\forall x \in [0;5]\)

nên \(\mathop {\max }\limits_{[0;5]} g\left( x \right) = \frac{{\mathop {\max }\limits_{[0;5]} h\left( x \right)}}{{\sqrt {\mathop {\min }\limits_{[0;5]} f\left( x \right)} }} = \frac{5}{1}\) tại \(x = 3\) và \[\mathop {\min }\limits_{[0;5]} g\left( x \right) = \frac{{\mathop {\min }\limits_{[0;5]} h\left( x \right)}}{{\sqrt {\mathop {\max }\limits_{[0;5]} f\left( x \right)} }} = \frac{{\sqrt {10} }}{{\sqrt {10} }} = 1\] tại \(x = 0\).

Để phương trình đã cho có nghiệm trên đoạn \(\left[ {0\,;\,5} \right]\) thì \(\mathop {\min }\limits_{[0;5]} g\left( x \right) \le m \le \mathop {\max }\limits_{[0;5]} g\left( x \right) \Leftrightarrow 1 \le m \le 5\).

Vậy có 5 giá trị của tham số \(m\).