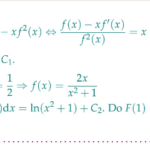Cho hàm số $f(x)$ có nguyên hàm $F(x)$ và thỏa mãn $x f^{\prime}(x)=f(x)-x f^{2}(x)$ với mọi $x \in(0 ;+\infty)$. Biết $f(1)=1$ và $F(1)=\ln 2$. Tính $F(2)$.A. $2 \ln 2$.B. $\ln 5$.C. $3 \ln 2$.D. $2 \ln 3$. … [Đọc thêm...] vềCho hàm số $f(x)$ có nguyên hàm $F(x)$ và thỏa mãn $x f^{\prime}(x)=f(x)-x f^{2}(x)$ với mọi $x \in(0 ;+\infty)$. Biết $f(1)=1$ và $F(1)=\ln 2$. Tính $F(2)$.
VDC Toan 2023
Cho khối nón đỉnh $S$ có đường cao bằng 2a. Mặt phẳng $(P)$ đi qua đỉnh $S$ nhưng không chứa trục của hình nón cắt đường tròn đáy tại hai điểm $A$ và $B$ sao cho $A B=4 a$. Biết mặt phẳng $(P)$ tạo với đáy nón một góc $60^{\circ}$, thể tính của khối nón đã cho bằng
Cho khối nón đỉnh $S$ có đường cao bằng 2a. Mặt phẳng $(P)$ đi qua đỉnh $S$ nhưng không chứa trục của hình nón cắt đường tròn đáy tại hai điểm $A$ và $B$ sao cho $A B=4 a$. Biết mặt phẳng $(P)$ tạo với đáy nón một góc $60^{\circ}$, thể tính của khối nón đã cho bằngA. $\frac{32 \pi a^{3}}{9}$.B. $32 \pi a^{3}$.C. $\frac{32 \pi a^{3}}{3}$.D. $\frac{64 \pi a^{3}}{9}$. Lời … [Đọc thêm...] vềCho khối nón đỉnh $S$ có đường cao bằng 2a. Mặt phẳng $(P)$ đi qua đỉnh $S$ nhưng không chứa trục của hình nón cắt đường tròn đáy tại hai điểm $A$ và $B$ sao cho $A B=4 a$. Biết mặt phẳng $(P)$ tạo với đáy nón một góc $60^{\circ}$, thể tính của khối nón đã cho bằng
Biết\(I = \int\limits_0^{\frac{\pi }{2}} {\frac{{{{\sin }^{2023}}x}}{{{{\sin }^{2023}}x + {{\cos }^{2023}}x}}{\rm{d}}x} = a\frac{\pi }{4} + b\) với \(a,b \in \mathbb{Z}\). Giá trị của biểu thức \(T = {a^2} + {b^2}\) bằng
Biết\(I = \int\limits_0^{\frac{\pi }{2}} {\frac{{{{\sin }^{2023}}x}}{{{{\sin }^{2023}}x + {{\cos }^{2023}}x}}{\rm{d}}x} = a\frac{\pi }{4} + b\) với \(a,b \in \mathbb{Z}\). Giá trị của biểu thức \(T = {a^2} + {b^2}\) bằng A. \(1\). B. \(4\). C. \(5\). D. \(10\). Lời giải: Xét \(I = \int\limits_0^{\frac{\pi }{2}} {\frac{{{{\sin }^{2023}}x}}{{{{\sin }^{2023}}x + … [Đọc thêm...] vềBiết\(I = \int\limits_0^{\frac{\pi }{2}} {\frac{{{{\sin }^{2023}}x}}{{{{\sin }^{2023}}x + {{\cos }^{2023}}x}}{\rm{d}}x} = a\frac{\pi }{4} + b\) với \(a,b \in \mathbb{Z}\). Giá trị của biểu thức \(T = {a^2} + {b^2}\) bằng
Cho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm trên đoạn \(\left[ { – 5;8} \right]\), biết\(f\left( { – 2} \right) + f\left( 2 \right) = \frac{{70}}{3}\). Đồ thị của \(f’\left( x \right)\) như hình vẽ được xác định là Parabol và đường thẳng trên đoạn đó. .Giá trị \(\int\limits_{ – 5}^8 {f\left( x \right){\rm{d}}x} \) là
Cho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm trên đoạn \(\left[ { - 5;8} \right]\), biết \(f\left( { - 2} \right) + f\left( 2 \right) = \frac{{70}}{3}\). Đồ thị của \(f'\left( x \right)\) như hình vẽ được xác định là Parabol và đường thẳng trên đoạn đó. .Giá trị \(\int\limits_{ - 5}^8 {f\left( x \right){\rm{d}}x} \) là A. \( - 90\) . B. … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm trên đoạn \(\left[ { – 5;8} \right]\), biết
\(f\left( { – 2} \right) + f\left( 2 \right) = \frac{{70}}{3}\). Đồ thị của \(f’\left( x \right)\) như hình vẽ được xác định là Parabol và đường thẳng trên đoạn đó. .Giá trị \(\int\limits_{ – 5}^8 {f\left( x \right){\rm{d}}x} \) là
Biết diện tích hình phẳng giới hạn bởi đồ thị các hàm số \(y = {x^2}\ln x\) , \(x = 2\) và trục hoành là \(S = \frac{{a\ln b}}{c} – \frac{d}{{{c^2}}}\) với \(a,b,c,d \in {\mathbb{N}^*}\) và \(b\) là số nguyên tố. Tính \(a + b + c +d\)
Biết diện tích hình phẳng giới hạn bởi đồ thị các hàm số \(y = {x^2}\ln x\) , \(x = 2\) và trục hoành là \(S = \frac{{a\ln b}}{c} - \frac{d}{{{c^2}}}\) với \(a,b,c,d \in {\mathbb{N}^*}\) và \(b\) là số nguyên tố. Tính \(a + b + c +d\) A. \(13\). B. \(10\). C. \(20\). D. \(18\). Lời giải: Phương trình hoành độ giao điểm của hai đồ thị hàm số trên … [Đọc thêm...] vềBiết diện tích hình phẳng giới hạn bởi đồ thị các hàm số \(y = {x^2}\ln x\) , \(x = 2\) và trục hoành là \(S = \frac{{a\ln b}}{c} – \frac{d}{{{c^2}}}\) với \(a,b,c,d \in {\mathbb{N}^*}\) và \(b\) là số nguyên tố. Tính \(a + b + c +d\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right)\) trên \(\mathbb{R}\) và đồ thị của hàm số \(f’\left( x \right)\) cắt trục hoành tại bốn điểm có hoành độ theo thứ tự từ trái sang phải trên trục hoành là \(a,0,\,b,\,c\) \(\left( {a < 0 < b < c} \right)\) như hình vẽ.Khẳng định nào đúng trong các khẳng định sau?
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) trên \(\mathbb{R}\) và đồ thị của hàm số \(f'\left( x \right)\) cắt trục hoành tại bốn điểm có hoành độ theo thứ tự từ trái sang phải trên trục hoành là \(a,0,\,b,\,c\) \(\left( {a < 0 < b < c} \right)\) như hình vẽ. Khẳng định nào đúng trong các khẳng định sau? A.\(f\left( c \right) > … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right)\) trên \(\mathbb{R}\) và đồ thị của hàm số \(f’\left( x \right)\) cắt trục hoành tại bốn điểm có hoành độ theo thứ tự từ trái sang phải trên trục hoành là \(a,0,\,b,\,c\) \(\left( {a < 0 < b < c} \right)\) như hình vẽ.
Khẳng định nào đúng trong các khẳng định sau?
Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là \(AB = 8\,\,{\rm{m}}{\rm{.}}\) Người ra treo một tâm phông hình chữ nhật có hai đỉnh \(M,\,\,N\)nằm trên Parabol và hai đỉnh \(P,\,\,Q\) nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí với chi phí cho \(1\,\,{{\rm{m}}^2}\) cần số tiền mua hoa là \(200.000\) đồng, biết \(MN = 4\,\,{\rm{m}},\,\,MQ = 6\,\,{\rm{m}}{\rm{.}}\) Hỏi số tiền dùng để mua hoa trang trí chiếc cổng gần với số tiền nào sau đây?
Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là \(AB = 8\,\,{\rm{m}}{\rm{.}}\) Người ra treo một tâm phông hình chữ nhật có hai đỉnh \(M,\,\,N\)nằm trên Parabol và hai đỉnh \(P,\,\,Q\) nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí với chi phí cho \(1\,\,{{\rm{m}}^2}\) cần số tiền mua hoa … [Đọc thêm...] vềMột chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là \(AB = 8\,\,{\rm{m}}{\rm{.}}\) Người ra treo một tâm phông hình chữ nhật có hai đỉnh \(M,\,\,N\)nằm trên Parabol và hai đỉnh \(P,\,\,Q\) nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí với chi phí cho \(1\,\,{{\rm{m}}^2}\) cần số tiền mua hoa là \(200.000\) đồng, biết \(MN = 4\,\,{\rm{m}},\,\,MQ = 6\,\,{\rm{m}}{\rm{.}}\) Hỏi số tiền dùng để mua hoa trang trí chiếc cổng gần với số tiền nào sau đây?
Cho hàm số \(y = f\left( x \right)\) có đạo hàm và liên tục trên đoạn \(\left[ {0;\,4} \right]\) thỏa mãn \(f\left( 2 \right) = 16\), \(\,\int\limits_0^2 {{{\left[ {f’\left( x \right)} \right]}^2}dx = \frac{{1814}}{{15}}} \) và \(\int\limits_0^4 {f\left( {\sqrt x } \right)dx} = \frac{1}{3}\). Tính diện tích hình phẳng giới hạn bởi các đường \(y = f(x),\,\,x = 1,\,\,x = 4\) và trục hoành.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm và liên tục trên đoạn \(\left[ {0;\,4} \right]\) thỏa mãn \(f\left( 2 \right) = 16\), \(\,\int\limits_0^2 {{{\left[ {f'\left( x \right)} \right]}^2}dx = \frac{{1814}}{{15}}} \) và \(\int\limits_0^4 {f\left( {\sqrt x } \right)dx} = \frac{1}{3}\). Tính diện tích hình phẳng giới hạn bởi các đường \(y = f(x),\,\,x = 1,\,\,x = 4\) và … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đạo hàm và liên tục trên đoạn \(\left[ {0;\,4} \right]\) thỏa mãn \(f\left( 2 \right) = 16\), \(\,\int\limits_0^2 {{{\left[ {f’\left( x \right)} \right]}^2}dx = \frac{{1814}}{{15}}} \) và \(\int\limits_0^4 {f\left( {\sqrt x } \right)dx} = \frac{1}{3}\). Tính diện tích hình phẳng giới hạn bởi các đường \(y = f(x),\,\,x = 1,\,\,x = 4\) và trục hoành.
Người ta tạo ra mô hình trang trí trong công viên bằng cách dùng một tấm mica hình dạng là nửa Elip có độ dài trục lớn DB là 10dm, độ dài trục bé là 8dm, vẽ thêm nửa đường tròn tâm là trung điểm của trục lớn DB, bán kính bằng 3dm ở bên trong, xác định 2 điểm A và C trên mép Elip sao cho \(\widehat {AOB} = \widehat {COD} = {45^0}\) (hình vẽ). Sau đó cắt bỏ đi một phần Elip giới hạn bởi 2 đoạn OA, OC, và hai phần của hình tròn bên trong. Người ta đặt một trục quay vào DB rồi quay hai phần mica còn lại (được đánh dấu) xung quanh BD tạo thành mô hình trang trí dạng tròn xoay. Phần không gian mà mô hình đó chiếm chỗ có giá trị gần nhất bằng:
Người ta tạo ra mô hình trang trí trong công viên bằng cách dùng một tấm mica hình dạng là nửa Elip có độ dài trục lớn DB là 10dm, độ dài trục bé là 8dm, vẽ thêm nửa đường tròn tâm là trung điểm của trục lớn DB, bán kính bằng 3dm ở bên trong, xác định 2 điểm A và C trên mép Elip sao cho \(\widehat {AOB} = \widehat {COD} = {45^0}\) (hình vẽ). Sau đó cắt bỏ đi một phần Elip giới … [Đọc thêm...] vềNgười ta tạo ra mô hình trang trí trong công viên bằng cách dùng một tấm mica hình dạng là nửa Elip có độ dài trục lớn DB là 10dm, độ dài trục bé là 8dm, vẽ thêm nửa đường tròn tâm là trung điểm của trục lớn DB, bán kính bằng 3dm ở bên trong, xác định 2 điểm A và C trên mép Elip sao cho \(\widehat {AOB} = \widehat {COD} = {45^0}\) (hình vẽ). Sau đó cắt bỏ đi một phần Elip giới hạn bởi 2 đoạn OA, OC, và hai phần của hình tròn bên trong. Người ta đặt một trục quay vào DB rồi quay hai phần mica còn lại (được đánh dấu) xung quanh BD tạo thành mô hình trang trí dạng tròn xoay. Phần không gian mà mô hình đó chiếm chỗ có giá trị gần nhất bằng:
Cho đường tròn tâm O có đường kính bằng \(4\) và Elip có phương trình: \(\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{4} = 1\) . Diện tích \(S\) phần hình phẳng ở bên ngoài đường tròn và bên trong Elip gần với kết quả nào nhất trong \(4\) kết quả dưới đây?
Cho đường tròn tâm O có đường kính bằng \(4\) và Elip có phương trình: \(\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{4} = 1\) . Diện tích \(S\) phần hình phẳng ở bên ngoài đường tròn và bên trong Elip gần với kết quả nào nhất trong \(4\) kết quả dưới đây? A. \(3,14\). B. \(15,71\). C. \(20\). D. \(18,85\). Lời giải: Ta có : \(\frac{{{x^2}}}{{25}} … [Đọc thêm...] vềCho đường tròn tâm O có đường kính bằng \(4\) và Elip có phương trình: \(\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{4} = 1\) . Diện tích \(S\) phần hình phẳng ở bên ngoài đường tròn và bên trong Elip gần với kết quả nào nhất trong \(4\) kết quả dưới đây?