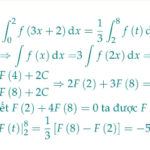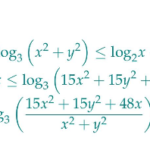VDC Toan 2023

Tập nghiệm S của bất phương trình ${\log _{\frac{2}{3}}}\left( {2x – 4} \right) + {\log _{\frac{2}{3}}}\left( {x + 3} \right) < {\log _{\frac{3}{2}}}\frac{1}{{28}}$ là

Ngày 11/06/2023 Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, Phuong trinh logarit, VDC Toan 2023

Tập nghiệm S của bất phương trình ${\log _{\frac{2}{3}}}\left( {2x - 4} \right) + {\log _{\frac{2}{3}}}\left( {x + 3} \right) < {\log _{\frac{3}{2}}}\frac{1}{{28}}$ là A. $S = \left( {4;\, + \infty } \right)$. B. $S = \left( {2;\;4} \right)$. C. $S = \left( { - 5;\;4} \right)$. D. $S = \left( { - \infty ;\; - 5} \right) \cup \left( {4;\; + \infty } … [Đọc thêm...] vềTập nghiệm S của bất phương trình \({\log _{\frac{2}{3}}}\left( {2x – 4} \right) + {\log _{\frac{2}{3}}}\left( {x + 3} \right) < {\log _{\frac{3}{2}}}\frac{1}{{28}}$ là

Có bao nhiêu giá trị nguyên của tham số $m \in \left[ {1\,;\,2023} \right]$ để phương trình $\left( {{4^{x + 1}} – 65 \cdot {2^x} + 16} \right) \cdot \sqrt {{{\log }_3}{x^2} – m} = 0$ có $2$ nghiệm nguyên.

Ngày 11/06/2023 Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, Phuong trinh logarit, VDC Toan 2023

Có bao nhiêu giá trị nguyên của tham số $m \in \left[ {1\,;\,2023} \right]$ để phương trình $\left( {{4^{x + 1}} - 65 \cdot {2^x} + 16} \right) \cdot \sqrt {{{\log }_3}{x^2} - m} = 0$ có $2$ nghiệm nguyên. A. $1012$. B. $1011$. C. $1$. D. $1010$. Lời giải: Đkxđ: $\left\{ \begin{array}{l}{x^2} > 0\\{\log _3}{x^2} - m \ge 0\end{array} \right. … [Đọc thêm...] vềCó bao nhiêu giá trị nguyên của tham số \(m \in \left[ {1\,;\,2023} \right]$ để phương trình $\left( {{4^{x + 1}} – 65 \cdot {2^x} + 16} \right) \cdot \sqrt {{{\log }_3}{x^2} – m} = 0$ có $2$ nghiệm nguyên.

Tìm các giá trị thực của tham số $m$ để phương trình $\log _2^2x – 5{\log _2}x + 2m – 6 = 0$ có hai nghiệm thực ${x_1};\,{x_2}$ thỏa mãn $\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right) = 60$.

Ngày 11/06/2023 Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, Phuong trinh logarit, VDC Toan 2023

Tìm các giá trị thực của tham số $m$ để phương trình $\log _2^2x - 5{\log _2}x + 2m - 6 = 0$ có hai nghiệm thực ${x_1};\,{x_2}$ thỏa mãn $\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right) = 60$. A. $m = 9$. B. $m = 3$. C. không tồn tại. D. $m = 6$. Lời giải: $\log _2^2x - 5{\log _2}x + 2m - 6 = 0\;\left( 1 \right)$ Điều kiện: $x > … [Đọc thêm...] vềTìm các giá trị thực của tham số \(m$ để phương trình $\log _2^2x – 5{\log _2}x + 2m – 6 = 0$ có hai nghiệm thực ${x_1};\,{x_2}$ thỏa mãn $\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right) = 60$.

Tìm $m$ để bất phương trình ${3^x} + {4^x} + {5^x} + {6^x} \ge 4 + mx$ có tập nghiệm là $\mathbb{R}$.

Ngày 11/06/2023 Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, Phuong trinh logarit, VDC Toan 2023

Tìm $m$ để bất phương trình ${3^x} + {4^x} + {5^x} + {6^x} \ge 4 + mx$ có tập nghiệm là $\mathbb{R}$. A. $m \in \left( {3;4} \right)$. B. $m \in \left( {4;5} \right)$. C. $m \in \left( {5;6} \right)$. D. $m \in \left( {6;7} \right)$. Lời giải: + Với $a > 1$ ta có $\mathop {\lim }\limits_{x \to 0} \frac{{{a^x} - 1}}{x} = \mathop {\lim … [Đọc thêm...] vềTìm \(m$ để bất phương trình ${3^x} + {4^x} + {5^x} + {6^x} \ge 4 + mx$ có tập nghiệm là $\mathbb{R}$.

Có bao nhiêu giá trị nguyên của tham số $m$ thuộc khoảng $\left( { – 2023\,;2023} \right)$ để phương trình ${3.6^x} – \left( {7m – 48} \right).\sqrt {{6^x}} + 2{m^2} – 16m = 0$ có hai nghiệm phân biệt ${x_1},{x_2}$ thỏa mãn ${x_1} + {x_2} \ge 2\,\,?$

Ngày 11/06/2023 Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, Phuong trinh logarit, VDC Toan 2023

Có bao nhiêu giá trị nguyên của tham số $m$ thuộc khoảng $\left( { - 2023\,;2023} \right)$ để phương trình ${3.6^x} - \left( {7m - 48} \right).\sqrt {{6^x}} + 2{m^2} - 16m = 0$ có hai nghiệm phân biệt ${x_1},{x_2}$ thỏa mãn ${x_1} + {x_2} \ge 2\,\,?$ A. $2023$. B. $4036$. C. $2022$. D. $2014$. Lời giải: • Xét phương trình: ${3.6^x} - \left( … [Đọc thêm...] vềCó bao nhiêu giá trị nguyên của tham số \(m$ thuộc khoảng $\left( { – 2023\,;2023} \right)$ để phương trình ${3.6^x} – \left( {7m – 48} \right).\sqrt {{6^x}} + 2{m^2} – 16m = 0$ có hai nghiệm phân biệt ${x_1},{x_2}$ thỏa mãn ${x_1} + {x_2} \ge 2\,\,?$

Một hộp chứa 12 quả cầu gồm 5 quả màu vàng được đánh số từ 1 đến 5 và 7quả màu xanh được đánh số từ 1 đến 7. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất đểlấy được hai quả khác màu đồng thời tích hai số ghi trên chúng lớn hơn 14 bằng

Ngày 30/05/2023 Thuộc chủ đề:Trắc nghiệm Xác suất Tag với:On thi to hop xac suat, VDC Toan 2023

Một hộp chứa 12 quả cầu gồm 5 quả màu vàng được đánh số từ 1 đến 5 và 7 quả màu xanh được đánh số từ 1 đến 7. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu đồng thời tích hai số ghi trên chúng lớn hơn 14 bằng A. $\frac{2}{11}$ B. $\frac{3}{22}$ C. $\frac{7}{33}$ D. $\frac{4}{33}$ LỜI GIẢI Chọn 2 quả cầu từ 12 quả cầu có n(Ω) = $C_2^12$ = 66 cách. Gọi … [Đọc thêm...] vềMột hộp chứa 12 quả cầu gồm 5 quả màu vàng được đánh số từ 1 đến 5 và 7quả màu xanh được đánh số từ 1 đến 7. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất đểlấy được hai quả khác màu đồng thời tích hai số ghi trên chúng lớn hơn 14 bằng

Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=3 f(2 x)$. Gọi $F(x)$ là nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)=3$ và $F(2)+4 F(8)=0$. Khi đó $\int_{0}^{2} f(3 x+2) \mathrm{d} x$ bằng

Ngày 30/05/2023 Thuộc chủ đề:Trắc nghiệm Tích phân Tag với:tich phan nang cao, VDC Toan 2023

Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=3 f(2 x)$. Gọi $F(x)$ là nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)=3$ và $F(2)+4 F(8)=0$. Khi đó $\int_{0}^{2} f(3 x+2) \mathrm{d} x$ bằngA. 5 .B. -5 .C. 3 .D. -3 . … [Đọc thêm...] vềCho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=3 f(2 x)$. Gọi $F(x)$ là nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)=3$ và $F(2)+4 F(8)=0$. Khi đó $\int_{0}^{2} f(3 x+2) \mathrm{d} x$ bằng

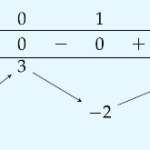
Biết $f(-1)=1$, hàm số $y=\left|f\left(x^{2}-2 x\right)\right|$ có bao nhiêu điểm cực trị? Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

Ngày 30/05/2023 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri ham hop, VDC Toan 2023

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau: Biết $f(-1)=1$, hàm số $y=\left|f\left(x^{2}-2 x\right)\right|$ có bao nhiêu điểm cực trị?A. 11.B. 9 .C. 15 .D. 7 . … [Đọc thêm...] vềBiết $f(-1)=1$, hàm số $y=\left|f\left(x^{2}-2 x\right)\right|$ có bao nhiêu điểm cực trị? Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn [-15; 15] để hàm số $y=\left|\frac{m x+5}{x+m}\right|$ dồng biến trên khoảng $(1 ; 10)$ ?

Ngày 30/05/2023 Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:Don dieu VDC, VDC Toan 2023

Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn [-15; 15] để hàm số $y=\left|\frac{m x+5}{x+m}\right|$ dồng biến trên khoảng $(1 ; 10)$ ? A. 12 . B. 13 . C. 18. D. 19 . … [Đọc thêm...] vềCó bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn [-15; 15] để hàm số $y=\left|\frac{m x+5}{x+m}\right|$ dồng biến trên khoảng $(1 ; 10)$ ?

Có bao nhiêu cặp số nguyên $(x ; y)$ thỏa mãn $\log {2}\left(x^{2}+y^{2}+4 x\right)+\log {3}\left(x^{2}+y^{2}\right) \leq \log {2} x+\log {3}\left(15 x^{2}+15 y^{2}+48 x\right) ?$

Ngày 28/05/2023 Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:Logarit nang cao, VDC Toan 2023

Câu 44: Có bao nhiêu cặp số nguyên $(x ; y)$ thỏa mãn $$\log _{2}\left(x^{2}+y^{2}+4 x\right)+\log _{3}\left(x^{2}+y^{2}\right) \leq \log _{2} x+\log _{3}\left(15 x^{2}+15 y^{2}+48 x\right) ?$$A. 22.B. 28 .C. 15 .D. 12 . … [Đọc thêm...] vềCó bao nhiêu cặp số nguyên $(x ; y)$ thỏa mãn $\log {2}\left(x^{2}+y^{2}+4 x\right)+\log {3}\left(x^{2}+y^{2}\right) \leq \log {2} x+\log {3}\left(15 x^{2}+15 y^{2}+48 x\right) ?$

Tập nghiệm S của bất phương trình \({\log _{\frac{2}{3}}}\left( {2x – 4} \right) + {\log _{\frac{2}{3}}}\left( {x + 3} \right) < {\log _{\frac{3}{2}}}\frac{1}{{28}}\) là

Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ {1\,;\,2023} \right]\) để phương trình \(\left( {{4^{x + 1}} – 65 \cdot {2^x} + 16} \right) \cdot \sqrt {{{\log }_3}{x^2} – m} = 0\) có \(2\) nghiệm nguyên.

Tìm các giá trị thực của tham số \(m\) để phương trình \(\log _2^2x – 5{\log _2}x + 2m – 6 = 0\) có hai nghiệm thực \({x_1};\,{x_2}\) thỏa mãn \(\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right) = 60\).

Tìm \(m\) để bất phương trình \({3^x} + {4^x} + {5^x} + {6^x} \ge 4 + mx\) có tập nghiệm là \(\mathbb{R}\).

Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \(\left( { – 2023\,;2023} \right)\) để phương trình \({3.6^x} – \left( {7m – 48} \right).\sqrt {{6^x}} + 2{m^2} – 16m = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \({x_1} + {x_2} \ge 2\,\,?\)

Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=3 f(2 x)$. Gọi $F(x)$ là nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)=3$ và $F(2)+4 F(8)=0$. Khi đó $\int_{0}^{2} f(3 x+2) \mathrm{d} x$ bằng

Biết $f(-1)=1$, hàm số $y=\left|f\left(x^{2}-2 x\right)\right|$ có bao nhiêu điểm cực trị? Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn [-15; 15] để hàm số $y=\left|\frac{m x+5}{x+m}\right|$ dồng biến trên khoảng $(1 ; 10)$ ?

Có bao nhiêu cặp số nguyên $(x ; y)$ thỏa mãn \(\log {2}\left(x^{2}+y^{2}+4 x\right)+\log {3}\left(x^{2}+y^{2}\right) \leq \log {2} x+\log {3}\left(15 x^{2}+15 y^{2}+48 x\right) ?\)