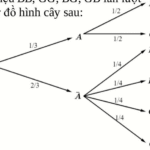
Bài toán: Một nhà máy có hai phân xưởng $A$ và $B$ tương ứng làm ra $60\\%$ và $40\\%$ sản phẩm của nhà máy. Tỉ lệ phế phẩm của hai phân xưởng A và B lần lượt là $1\\%$ và $2\\%$. Chọn ngẫu nhiên một sản phẩm của nhà máy.a) Nếu sản phẩm chọn ra thuộc phân xưởng A thì xác suất để nó không là phế phẩm là 0,98 .b) Xác suất để sản phẩm chọn ra là phế phẩm và thuộc phân xưởng A là … [Đọc thêm...] vềMột nhà máy có hai phân xưởng $A$ và $B$ tương ứng làm ra 60% và 40% sản phẩm của nhà máy. Tỉ lệ phế phẩm của hai phân xưởng A và B lần lượt là 1% và 2%. Chọn ngẫu nhiên một sản phẩm của nhà máy
Trắc nghiệm Xác suất
Cho một hộp bi thứ nhất đựng 6 viên bi đôi một khác nhau gồm: 2 viên bi màu xanh, 2 viên bi màu đỏ và 2 viên bi màu vàng. Các viên bi được xếp ngẫu nhiên thành một hàng ngang.
Bài toán: Cho một hộp bi thứ nhất đựng 6 viên bi đôi một khác nhau gồm: 2 viên bi màu xanh, 2 viên bi màu đỏ và 2 viên bi màu vàng. Các viên bi được xếp ngẫu nhiên thành một hàng ngang.a) Tổng số cách xếp 6 viên bi khác nhau thành một hàng ngang là 720 cáchb) Xác suất để hai viên bi màu xanh đứng cạnh nhau khi xếp ngẫu nhiên 6 viên bi là $\dfrac{1}{3}$c) Xác suất để hai viên bi … [Đọc thêm...] vềCho một hộp bi thứ nhất đựng 6 viên bi đôi một khác nhau gồm: 2 viên bi màu xanh, 2 viên bi màu đỏ và 2 viên bi màu vàng. Các viên bi được xếp ngẫu nhiên thành một hàng ngang.
Có hai đội tham gia một cuộc thi bơi lội. Đội I có 7 vận động viên, đội II có 9 vận động viên. Xác suất giành huy chương vàng của mỗi vận động viên đội I và đội II lần lượt là 0.07 và 0.06 . Chọn ngẫu nhiên một vận động viên (Kết quả làm tròn đến hàng phần trăm)
Bài toán: Có hai đội tham gia một cuộc thi bơi lội. Đội I có 7 vận động viên, đội II có 9 vận động viên. Xác suất giành huy chương vàng của mỗi vận động viên đội I và đội II lần lượt là 0.07 và 0.06 . Chọn ngẫu nhiên một vận động viên (Kết quả làm tròn đến hàng phần trăm)a) Xác suất để vận động viên được chọn thuộc đội I là 0,56b) Xác suất để vận động viên này không giành được … [Đọc thêm...] vềCó hai đội tham gia một cuộc thi bơi lội. Đội I có 7 vận động viên, đội II có 9 vận động viên. Xác suất giành huy chương vàng của mỗi vận động viên đội I và đội II lần lượt là 0.07 và 0.06 . Chọn ngẫu nhiên một vận động viên (Kết quả làm tròn đến hàng phần trăm)
Song sinh có thể là cùng trứng (identical) hoặc khác trứng (fraternal). Biết rằng $1/3$ số cặp song sinh là cùng trứng. Hiển nhiên, song sinh cùng trứng phải cùng giới tính; song sinh khác trứng có thể cùng hoặc khác giới tính.
Bài toán: Song sinh có thể là cùng trứng (identical) hoặc khác trứng (fraternal). Biết rằng $1/3$ số cặp song sinh là cùng trứng. Hiển nhiên, song sinh cùng trứng phải cùng giới tính; song sinh khác trứng có thể cùng hoặc khác giới tính. Giả sử song sinh cùng trứng có xác suất là hai bé trai hoặc hai bé gái như nhau, trong khi với song sinh khác trứng thì tất cả bốn khả năng … [Đọc thêm...] vềSong sinh có thể là cùng trứng (identical) hoặc khác trứng (fraternal). Biết rằng $1/3$ số cặp song sinh là cùng trứng. Hiển nhiên, song sinh cùng trứng phải cùng giới tính; song sinh khác trứng có thể cùng hoặc khác giới tính.
Một lô hạt giống được thu gom từ ba nguồn khác nhau. Nguồn I chiếm $\dfrac{1}{2}$ số hạt của lô, nguồn II chiếm $\dfrac{1}{3}$ số hạt của lô, còn lại là nguồn III. Tỉ lệ hạt nảy mầm đối với các hạt thuộc các nguồn I, II, III tương ứng là $90\mathrm{\,\% },80\mathrm{\,\% },70\mathrm{\,\% }$. Lấy ngẫu nhiên 1 hạt.
Bài toán: Một lô hạt giống được thu gom từ ba nguồn khác nhau. Nguồn I chiếm $\dfrac{1}{2}$ số hạt của lô, nguồn II chiếm $\dfrac{1}{3}$ số hạt của lô, còn lại là nguồn III. Tỉ lệ hạt nảy mầm đối với các hạt thuộc các nguồn I, II, III tương ứng là $90\mathrm{\,\% },80\mathrm{\,\% },70\mathrm{\,\% }$. Lấy ngẫu nhiên 1 hạt. a) Hạt lấy ra là hạt nảy mầm với xác suất là … [Đọc thêm...] vềMột lô hạt giống được thu gom từ ba nguồn khác nhau. Nguồn I chiếm $\dfrac{1}{2}$ số hạt của lô, nguồn II chiếm $\dfrac{1}{3}$ số hạt của lô, còn lại là nguồn III. Tỉ lệ hạt nảy mầm đối với các hạt thuộc các nguồn I, II, III tương ứng là $90\mathrm{\,\% },80\mathrm{\,\% },70\mathrm{\,\% }$. Lấy ngẫu nhiên 1 hạt.
Có hai hộp bóng $A$ và $B$ chỉ đựng các quả bóng đỏ và trắng, trong đó hộp $B$ đựng 4 quả bóng đỏ và 5 quả bóng trắng; tổng số bóng hai hộp không qua 20. Xét hai phép thử ngẫu nhiên sau:
Bài toán: Có hai hộp bóng $A$ và $B$ chỉ đựng các quả bóng đỏ và trắng, trong đó hộp $B$ đựng 4 quả bóng đỏ và 5 quả bóng trắng; tổng số bóng hai hộp không qua 20. Xét hai phép thử ngẫu nhiên sau: Phép thử thứ nhất: Lấy ngẫu nhiên 1 quả bóng từ hộp $A$ bỏ vào hộp $B$ rồi lấy ngẫu nhiên 1 quả bóng từ hộp B . Bằng thực nghiệm người ta biết được rằng khả năng lấy được quả bóng … [Đọc thêm...] vềCó hai hộp bóng $A$ và $B$ chỉ đựng các quả bóng đỏ và trắng, trong đó hộp $B$ đựng 4 quả bóng đỏ và 5 quả bóng trắng; tổng số bóng hai hộp không qua 20. Xét hai phép thử ngẫu nhiên sau:
Có hai hộp bút, hộp thứ nhất đựng 5 chiếc bút đỏ và 4 chiếc bút xanh, hộp thứ hai đựng 4 chiếc bút đỏ và 6 chiếc bút xanh, tất cả những chiếc bút đều có cùng hình dạng, kích thước và khối lượng
Bài toán: Có hai hộp bút, hộp thứ nhất đựng 5 chiếc bút đỏ và 4 chiếc bút xanh, hộp thứ hai đựng 4 chiếc bút đỏ và 6 chiếc bút xanh, tất cả những chiếc bút đều có cùng hình dạng, kích thước và khối lượng. Lấy ngẫu nhiên một chiếc bút từ hộp thứ nhất chuyển sang hộp thứ hai, sau đó lấy ngẫu nhiên một chiếc bút từ hộp thứ hai. a) Xác suất để chiếc bút lấy từ hộp thứ nhất có … [Đọc thêm...] vềCó hai hộp bút, hộp thứ nhất đựng 5 chiếc bút đỏ và 4 chiếc bút xanh, hộp thứ hai đựng 4 chiếc bút đỏ và 6 chiếc bút xanh, tất cả những chiếc bút đều có cùng hình dạng, kích thước và khối lượng
Một xí nghiệp sản xuất sản phẩm có tỉ lệ phế phẩm là $5\mathrm{\,\% }$. Mỗi sản phẩm sau khi sản xuất đều phải trải qua hai trạm kiểm tra độc lập. Cho biết ở trạm thứ nhất, xác suất nhận biết đúng với chính phẩm là 0,9 ; xác suất không nhận biết được phế phẩm là 0,03
Bài toán. Một xí nghiệp sản xuất sản phẩm có tỉ lệ phế phẩm là $5\mathrm{\,\% }$. Mỗi sản phẩm sau khi sản xuất đều phải trải qua hai trạm kiểm tra độc lập. Cho biết ở trạm thứ nhất, xác suất nhận biết đúng với chính phẩm là 0,9 ; xác suất không nhận biết được phế phẩm là 0,03 . Còn ở trạm thứ hai, xác suất nhận biết đúng chính phẩm là 0,95 ; xác suất không nhận biết được phế … [Đọc thêm...] vềMột xí nghiệp sản xuất sản phẩm có tỉ lệ phế phẩm là $5\mathrm{\,\% }$. Mỗi sản phẩm sau khi sản xuất đều phải trải qua hai trạm kiểm tra độc lập. Cho biết ở trạm thứ nhất, xác suất nhận biết đúng với chính phẩm là 0,9 ; xác suất không nhận biết được phế phẩm là 0,03
Kết quả 40 lần nhảy xa của hai vận động viên (VĐV) Hùng và Đạt được lần lượt thống kê trong bảng 1 và bảng 2 dưới đây (đơn vị: mét):
Bài toán: Kết quả 40 lần nhảy xa của hai vận động viên (VĐV) Hùng và Đạt được lần lượt thống kê trong bảng 1 và bảng 2 dưới đây (đơn vị: mét): Bảng 1 (VĐV Hùng): Nhóm$\left[6,22;6,46\right)$$\left[6,46;6,70\right)$$\left[6,70;6,94\right)$$\left[6,94;7,18\right)$$\left[7,18;7,42\right)$Tần số375205 Bảng 2 (VĐV … [Đọc thêm...] vềKết quả 40 lần nhảy xa của hai vận động viên (VĐV) Hùng và Đạt được lần lượt thống kê trong bảng 1 và bảng 2 dưới đây (đơn vị: mét):
Người ta đem nhốt ngẫu nhiên 9 con thỏ trong đó có 3 con thỏ lông màu trắng, 3 con thỏ lông màu vàng, 3 con thỏ lông màu đen vào 3 cái chuồng khác nhau, mỗi chuồng có 3 con. Gọi $A$ là biến cố không có 3 con thỏ cùng màu lông nhốt chung 1 chuồng. Tính xác suất của biến cố $A$.
Người ta đem nhốt ngẫu nhiên 9 con thỏ trong đó có 3 con thỏ lông màu trắng, 3 con thỏ lông màu vàng, 3 con thỏ lông màu đen vào 3 cái chuồng khác nhau, mỗi chuồng có 3 con. Gọi $A$ là biến cố không có 3 con thỏ cùng màu lông nhốt chung 1 chuồng. Tính xác suất của biến cố $A$. LỜI GIẢI Nhốt 9 con thỏ vào 3 chuồng mỗi chuồng có 3 con thỏ, số phần tử của không gian mẫu là … [Đọc thêm...] vềNgười ta đem nhốt ngẫu nhiên 9 con thỏ trong đó có 3 con thỏ lông màu trắng, 3 con thỏ lông màu vàng, 3 con thỏ lông màu đen vào 3 cái chuồng khác nhau, mỗi chuồng có 3 con. Gọi $A$ là biến cố không có 3 con thỏ cùng màu lông nhốt chung 1 chuồng. Tính xác suất của biến cố $A$.