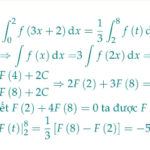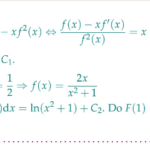tich phan nang cao

Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=3 f(2 x)$. Gọi $F(x)$ là nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)=3$ và $F(2)+4 F(8)=0$. Khi đó $\int_{0}^{2} f(3 x+2) \mathrm{d} x$ bằng

Ngày 30/05/2023 Thuộc chủ đề:Trắc nghiệm Tích phân Tag với:tich phan nang cao, VDC Toan 2023

Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=3 f(2 x)$. Gọi $F(x)$ là nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)=3$ và $F(2)+4 F(8)=0$. Khi đó $\int_{0}^{2} f(3 x+2) \mathrm{d} x$ bằngA. 5 .B. -5 .C. 3 .D. -3 . … [Đọc thêm...] vềCho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=3 f(2 x)$. Gọi $F(x)$ là nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)=3$ và $F(2)+4 F(8)=0$. Khi đó $\int_{0}^{2} f(3 x+2) \mathrm{d} x$ bằng

Cho hàm số $f(x)$ có nguyên hàm $F(x)$ và thỏa mãn $x f^{\prime}(x)=f(x)-x f^{2}(x)$ với mọi $x \in(0 ;+\infty)$. Biết $f(1)=1$ và $F(1)=\ln 2$. Tính $F(2)$.

Ngày 28/05/2023 Thuộc chủ đề:Trắc nghiệm Tích phân Tag với:tich phan nang cao, VDC Toan 2023

Cho hàm số $f(x)$ có nguyên hàm $F(x)$ và thỏa mãn $x f^{\prime}(x)=f(x)-x f^{2}(x)$ với mọi $x \in(0 ;+\infty)$. Biết $f(1)=1$ và $F(1)=\ln 2$. Tính $F(2)$.A. $2 \ln 2$.B. $\ln 5$.C. $3 \ln 2$.D. $2 \ln 3$. … [Đọc thêm...] vềCho hàm số $f(x)$ có nguyên hàm $F(x)$ và thỏa mãn $x f^{\prime}(x)=f(x)-x f^{2}(x)$ với mọi $x \in(0 ;+\infty)$. Biết $f(1)=1$ và $F(1)=\ln 2$. Tính $F(2)$.

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$. Gọi $F\left( x \right),G\left( x \right)$ là hai nguyên hàm của $f\left( x \right)$ trên $\mathbb{R}$ thỏa mãn $F\left( 4 \right) + G\left( 4 \right) = 4$ và $F\left( 0 \right) + G\left( 0 \right) = 1$. Khi đó $\int\limits_0^2 f \left( {2x} \right){\rm{d}}x$ bằng

Ngày 11/03/2023 Thuộc chủ đề:Trắc nghiệm Tích phân Tag với:tich phan nang cao

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ . Gọi $F\left( x \right),G\left( x \right)$ là hai nguyên hàm của $f\left( x \right)$ trên $\mathbb{R}$ thỏa mãn $F\left( 4 \right) + G\left( 4 \right) = 4$ và $F\left( 0 \right) + G\left( 0 \right) = 1$ . Khi đó $\int\limits_0^2 f \left( {2x} \right){\rm{d}}x$ bằng B. 3. B. … [Đọc thêm...] vềCho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$. Gọi $F\left( x \right),G\left( x \right)$ là hai nguyên hàm của $f\left( x \right)$ trên $\mathbb{R}$ thỏa mãn $F\left( 4 \right) + G\left( 4 \right) = 4$ và $F\left( 0 \right) + G\left( 0 \right) = 1$. Khi đó $\int\limits_0^2 f \left( {2x} \right){\rm{d}}x$ bằng

(Sở Ninh Bình 2022) Cho hàm số $f(x) = {x^5} + a{x^4} + b{x^3} + c{x^2} + dx + 36$. Biết đồ thị hàm số $y = f(x),y = f\prime (x)$ và $Ox$ giao nhau tại hai điểm phân biệt có hoành độ lần lượt là 2,3. Diện tích hình phẳng giớihạn bởi đồ thị hàm số $y = f(x)$ và $Ox$ bằng $\frac{m}{n}$ là một phân số tối giản với $m,n \in {\mathbb{N}^*}$. Tổng $m + n$ bằng

Ngày 14/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:tich phan nang cao, Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: (Sở Ninh Bình 2022) Cho hàm số $f(x) = {x^5} + a{x^4} + b{x^3} + c{x^2} + dx + 36$. Biết đồ thị hàm số $y = f(x),y = f\prime (x)$ và $Ox$ giao nhau tại hai điểm phân biệt có hoành độ lần lượt là 2,3. Diện tích hình phẳng giớihạn bởi đồ thị hàm số $y = f(x)$ và $Ox$ bằng $\frac{m}{n}$ là một phân số tối giản với $m,n \in {\mathbb{N}^*}$. Tổng \(m + … [Đọc thêm...] về

(Sở Ninh Bình 2022) Cho hàm số $f(x) = {x^5} + a{x^4} + b{x^3} + c{x^2} + dx + 36$. Biết đồ thị hàm số $y = f(x),y = f\prime (x)$ và $Ox$ giao nhau tại hai điểm phân biệt có hoành độ lần lượt là 2,3. Diện tích hình phẳng giớihạn bởi đồ thị hàm số $y = f(x)$ và $Ox$ bằng $\frac{m}{n}$ là một phân số tối giản với $m,n \in {\mathbb{N}^*}$. Tổng $m + n$ bằng

(Chuyên Lam Sơn 2022) Cho hàm số $y = f(x)$ liên tục trên đoạn $\left[ {0;\frac{\pi }{2}} \right]$ thỏa mãn
$2\cos x \cdot f(1 + 4\sin x) – \sin 2x \cdot f(3 – 2\cos 2x) = \sin 4x + 4\sin 2x – 4\cos x,\forall x \in \left[ {0;\frac{\pi }{2}} \right]$
Khi đó $I = \int_1^5 f (x)dx$ bằng

Ngày 14/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:tich phan nang cao, Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: (Chuyên Lam Sơn 2022) Cho hàm số $y = f(x)$ liên tục trên đoạn $\left[ {0;\frac{\pi }{2}} \right]$ thỏa mãn $2\cos x \cdot f(1 + 4\sin x) - \sin 2x \cdot f(3 - 2\cos 2x) = \sin 4x + 4\sin 2x - 4\cos x,\forall x \in \left[ {0;\frac{\pi }{2}} \right]$ Khi đó $I = \int_1^5 f (x)dx$ bằng A. 2. B. 0. C. 8. D. 16. Lời giải: Ta có: … [Đọc thêm...] về

(Chuyên Lam Sơn 2022) Cho hàm số $y = f(x)$ liên tục trên đoạn $\left[ {0;\frac{\pi }{2}} \right]$ thỏa mãn

$2\cos x \cdot f(1 + 4\sin x) – \sin 2x \cdot f(3 – 2\cos 2x) = \sin 4x + 4\sin 2x – 4\cos x,\forall x \in \left[ {0;\frac{\pi }{2}} \right]$

Khi đó $I = \int_1^5 f (x)dx$ bằng

(Sở Hà Tĩnh 2022) Cho hàm số $f\left( x \right) = a{x^4} – {x^3} + 2x + 2$ và hàm số $g\left( x \right) = b{x^3} – c{x^2} + 2$ có đồ thị như hình vẽ bên. Gọi ${S_1};\,{S_2}$ là diện tích các hình phẳng gạch chéo trong hình vẽ, biết ${S_1} = \frac{{221}}{{640}}$. Khi đó ${S_2}$ bằng

Ngày 14/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:tich phan nang cao, Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: (Sở Hà Tĩnh 2022) Cho hàm số $f\left( x \right) = a{x^4} - {x^3} + 2x + 2$ và hàm số $g\left( x \right) = b{x^3} - c{x^2} + 2$ có đồ thị như hình vẽ bên. Gọi ${S_1};\,{S_2}$ là diện tích các hình phẳng gạch chéo trong hình vẽ, biết ${S_1} = \frac{{221}}{{640}}$. Khi đó ${S_2}$ bằng A. $\frac{{791}}{{640}}$. B. $\frac{{571}}{{640}}$. C. … [Đọc thêm...] về

(Sở Hà Tĩnh 2022) Cho hàm số $f\left( x \right) = a{x^4} – {x^3} + 2x + 2$ và hàm số $g\left( x \right) = b{x^3} – c{x^2} + 2$ có đồ thị như hình vẽ bên. Gọi ${S_1};\,{S_2}$ là diện tích các hình phẳng gạch chéo trong hình vẽ, biết ${S_1} = \frac{{221}}{{640}}$. Khi đó ${S_2}$ bằng

(THPT Lương Thế Vinh – Hà Nội – 2022) Một téc nước hình trụ, đang chứa nước được đạat nằm ngang, có chiều dài $3m$ và đường kính đáy $1m$. Hiện tại mặt nước trong téc cách phía trển đỉnh của téc $0,25\;m$ (xem hình vẽ). Tính thể tích của nước trong téc (kết quả làm tròn đến hàng phần nghìn)?

Ngày 14/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:tich phan nang cao, Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: (THPT Lương Thế Vinh – Hà Nội – 2022) Một téc nước hình trụ, đang chứa nước được đạat nằm ngang, có chiều dài $3m$ và đường kính đáy $1m$. Hiện tại mặt nước trong téc cách phía trển đỉnh của téc $0,25\;m$ (xem hình vẽ). Tính thể tích của nước trong téc (kết quả làm tròn đến hàng phần nghìn)? A. $1,768\;{m^3}$. B. $1,167{m^3}$ C. … [Đọc thêm...] về(THPT Lương Thế Vinh – Hà Nội – 2022) Một téc nước hình trụ, đang chứa nước được đạat nằm ngang, có chiều dài $3m$ và đường kính đáy $1m$. Hiện tại mặt nước trong téc cách phía trển đỉnh của téc $0,25\;m$ (xem hình vẽ). Tính thể tích của nước trong téc (kết quả làm tròn đến hàng phần nghìn)?

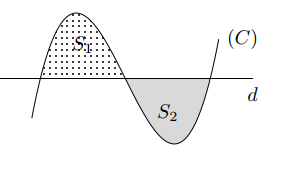
(Sở Ninh Bình 2022) Gọi $X$ là tập hợp tất cả các giá trị của tham số $m$ để đường thẳng $d$: $y = – 45m – 2$ cùng với đồ thị $(C)$ của hàm số $y = \frac{1}{3}{x^3} – 2m{x^2} + x + 1$ tạo thành hai miền kín có diện tích lần lượt là ${S_1},{S_2}$ thỏa mãn ${S_1} = {S_2}$ (xem hình vẽ). Số phần tử của tập $X$ là

Ngày 14/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:tich phan nang cao, Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: (Sở Ninh Bình 2022) Gọi $X$ là tập hợp tất cả các giá trị của tham số $m$ để đường thẳng $d$: $y = - 45m - 2$ cùng với đồ thị $(C)$ của hàm số $y = \frac{1}{3}{x^3} - 2m{x^2} + x + 1$ tạo thành hai miền kín có diện tích lần lượt là ${S_1},{S_2}$ thỏa mãn ${S_1} = {S_2}$ (xem hình vẽ). Số phần tử của tập $X$ là A. 0. B. 2. C. … [Đọc thêm...] về

(Sở Ninh Bình 2022) Gọi $X$ là tập hợp tất cả các giá trị của tham số $m$ để đường thẳng $d$: $y = – 45m – 2$ cùng với đồ thị $(C)$ của hàm số $y = \frac{1}{3}{x^3} – 2m{x^2} + x + 1$ tạo thành hai miền kín có diện tích lần lượt là ${S_1},{S_2}$ thỏa mãn ${S_1} = {S_2}$ (xem hình vẽ). Số phần tử của tập $X$ là

(THPT Bùi Thị Xuân – Huế – 2022) Một công ty có ý định thiết kế một logo hình vuông có độ dài nửa đường chéo bằng 4. Biểu tượng 4 chiếc lá (được tô màu) được tạo thành bởi các đường cong đối xứng với nhau qua tâm của hình vuông và qua các đường chéo.
Một trong số các đường cong ở nửa bên phải của logo là một phần của đồ thị hàm số bậc ba dạng $y = a{x^3} + b{x^2} – x$ với hệ số $a < 0$. Để kỷ niệm ngày thành lập $2/3$, công ty thiết kế để tỉ số diện tích được tô màu so với phần không được tô màu bằng $\frac{2}{3}$. Tính $2a + 2b$

Ngày 14/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:tich phan nang cao, Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: (THPT Bùi Thị Xuân – Huế - 2022) Một công ty có ý định thiết kế một logo hình vuông có độ dài nửa đường chéo bằng 4. Biểu tượng 4 chiếc lá (được tô màu) được tạo thành bởi các đường cong đối xứng với nhau qua tâm của hình vuông và qua các đường chéo. Một trong số các đường cong ở nửa bên phải của logo là một phần của đồ thị hàm số bậc ba dạng \(y = a{x^3} + … [Đọc thêm...] về

(THPT Bùi Thị Xuân – Huế – 2022) Một công ty có ý định thiết kế một logo hình vuông có độ dài nửa đường chéo bằng 4. Biểu tượng 4 chiếc lá (được tô màu) được tạo thành bởi các đường cong đối xứng với nhau qua tâm của hình vuông và qua các đường chéo.

Một trong số các đường cong ở nửa bên phải của logo là một phần của đồ thị hàm số bậc ba dạng $y = a{x^3} + b{x^2} – x$ với hệ số $a < 0$. Để kỷ niệm ngày thành lập $2/3$, công ty thiết kế để tỉ số diện tích được tô màu so với phần không được tô màu bằng $\frac{2}{3}$. Tính $2a + 2b$

(THPT Đô Lương – Nghệ An – 2022) Cho hàm số $y = f(x)$ liên tục trên $\left[ { – 1,1} \right]$ và thỏa mãn $f(x) + 2 = \frac{3}{2}\int_{ – 1}^1 {(x + t)} f(t)dt$. với $\forall x \in [ – 1;1]$ Tính tích phân $I = \int_{ – 1}^1 f (x)dx$

Ngày 14/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:tich phan nang cao, Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: (THPT Đô Lương – Nghệ An – 2022) Cho hàm số $y = f(x)$ liên tục trên $\left[ { - 1,1} \right]$ và thỏa mãn $f(x) + 2 = \frac{3}{2}\int_{ - 1}^1 {(x + t)} f(t)dt$. với $\forall x \in [ - 1;1]$ Tính tích phân $I = \int_{ - 1}^1 f (x)dx$ A. $I = 3$ B. $l = 4$ C. $I = 2$ D. $\mathfrak{l} = 1$ Lời giải: \(\int_{ - 1}^1 {(x + t)} … [Đọc thêm...] về

(THPT Đô Lương – Nghệ An – 2022) Cho hàm số $y = f(x)$ liên tục trên $\left[ { – 1,1} \right]$ và thỏa mãn $f(x) + 2 = \frac{3}{2}\int_{ – 1}^1 {(x + t)} f(t)dt$. với $\forall x \in [ – 1;1]$ Tính tích phân $I = \int_{ – 1}^1 f (x)dx$