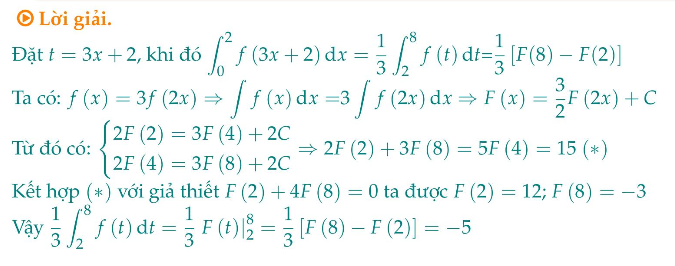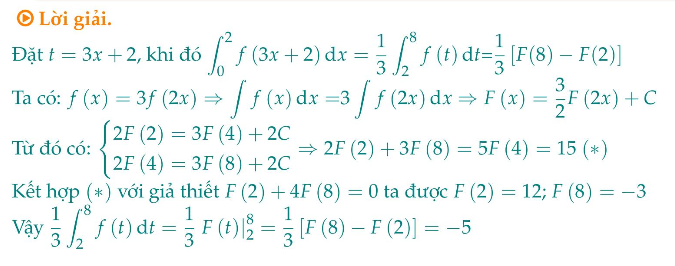
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=3 f(2 x)$. Gọi $F(x)$ là nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)=3$ và $F(2)+4 F(8)=0$. Khi đó $\int_{0}^{2} f(3 x+2) \mathrm{d} x$ bằng

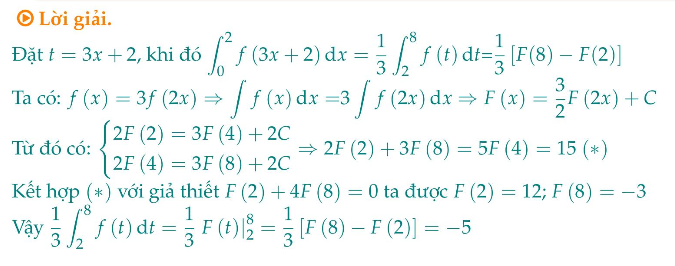
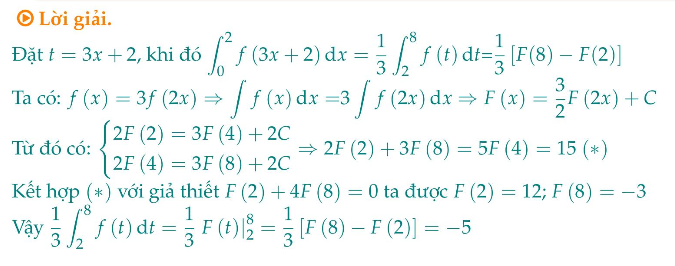
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=3 f(2 x)$. Gọi $F(x)$ là nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)=3$ và $F(2)+4 F(8)=0$. Khi đó $\int_{0}^{2} f(3 x+2) \mathrm{d} x$ bằng
A. 5 .
B. -5 .
C. 3 .
D. -3 .