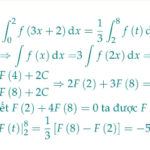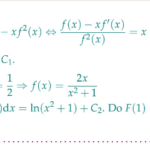ĐỀ BÀI (Chuyên Lê Quý Đôn – Đà Nẵng 2025) Một người đang điều khiển xe máy với vận tốc là $36\mathrm{\,\;km}/\mathrm{\,h}$ thì phát hiện đèn tín hiệu giao thông chuyển đỏ cách vị trí xe 80 m . Ba giây sau đó, xe máy bắt đầu giảm tốc với vận tốc được cho bởi […]
Trắc nghiệm Tích phân
Một bể bơi hình trụ có đường kính 5 m và chiều cao 1 m ; bể được bơm nước vào với tốc độ không đổi $v_{0}$. Sau khi nước được bơm đầy, bể bơi bị thủng một lỗ ở đáy và nước chảy ra ngoài; bể bơi chảy hết nước trong 8 giờ. Biết tốc độ giảm chiều cao của bể bơi khi nước chảy ra ngoài vào thời điểm $t$ giờ (tính từ lúc nước đầy bể và ngừng bơm) được cho bởi hàm số $h’\left(t\right)=at+b$, với $a,b\in \mathbb{R}$. Lúc nước chảy hết ra ngoài thì tốc độ giảm chiều cao bằng 0 .
ĐỀ BÀI Một bể bơi hình trụ có đường kính 5 m và chiều cao 1 m ; bể được bơm nước vào với tốc độ không đổi $v_{0}$. Sau khi nước được bơm đầy, bể bơi bị thủng một lỗ ở đáy và nước chảy ra ngoài; bể bơi chảy hết nước trong 8 […]
Thể tích nước của một bể bơi sau $t$ phút bơm tính theo công thức $V\left(t\right)=\dfrac{1}{100}\left(30t^{3}-\dfrac{t^{4}}{4}\right)$ (lít) với $\left(0\leq t\leq 90\right)$. Tốc độ bơm nước tại thời điểm $t$ được tính bởi công thức $f\left(t\right)=V’\left(t\right)$.
ĐỀ BÀI Thể tích nước của một bể bơi sau $t$ phút bơm tính theo công thức $V\left(t\right)=\dfrac{1}{100}\left(30t^{3}-\dfrac{t^{4}}{4}\right)$ (lít) với $\left(0\leq t\leq 90\right)$. Tốc độ bơm nước tại thời điểm $t$ được tính bởi công thức $f\left(t\right)=V’\left(t\right)$. Lời giải a) Thể tích nước của bể bơi sau 20 phút bơm là 2000 lít b) Tốc […]
Một quần thể vi khuẩn A có số lượng cá thề là $P\left( t \right)$ sau $t$ phút quan sát được phát hiện thay đồi với tốc độ là: ${P}’\left( t \right)=a{{e}^{0.1t}}+150{{e}^{-0.03t}}$ (vi khuẩn/phút) $\left( a\in \mathbb{R} \right)$. Biết rằng lúc bắt đầu quan sát, quần thể có 200000 vi khuẩn và đạt tốc độ tăng trường là 350 vi khuẩn/phút.
ĐỀ BÀI Một quần thể vi khuẩn A có số lượng cá thề là $P\left( t \right)$ sau $t$ phút quan sát được phát hiện thay đồi với tốc độ là: ${P}’\left( t \right)=a{{e}^{0.1t}}+150{{e}^{-0.03t}}$ (vi khuẩn/phút) $\left( a\in \mathbb{R} \right)$. Biết rằng lúc bắt đầu quan sát, quần thể có 200000 vi khuẩn và đạt […]
Một chất điểm chuyển động trong 3 giây với vận tốc $v\left( t \right)=m\text{cos}\left( \pi t \right)+n\left( on\text{ }\!\!~\!\!\text{ }vi:\text{ }\!\!~\!\!\text{ m}/\text{s} \right)$ trong đó $t$ (giây) là biến thời gian và $m,n$ là các hằng số có đồ thị như hình sin vẽ dưới đây:
ĐỀ BÀI Một chất điểm chuyển động trong 3 giây với vận tốc $v\left( t \right)=m\text{cos}\left( \pi t \right)+n\left( on\text{ }\!\!~\!\!\text{ }vi:\text{ }\!\!~\!\!\text{ m}/\text{s} \right)$ trong đó $t$ (giây) là biến thời gian và $m,n$ là các hằng số có đồ thị như hình sin vẽ dưới đây: Lời giải a) Vận tốc của vật […]
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=3 f(2 x)$. Gọi $F(x)$ là nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)=3$ và $F(2)+4 F(8)=0$. Khi đó $\int_{0}^{2} f(3 x+2) \mathrm{d} x$ bằng
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=3 f(2 x)$. Gọi $F(x)$ là nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)=3$ và $F(2)+4 F(8)=0$. Khi đó $\int_{0}^{2} f(3 x+2) \mathrm{d} x$ bằngA. 5 .B. -5 .C. 3 .D. -3 .
Cho hàm số $f(x)$ có nguyên hàm $F(x)$ và thỏa mãn $x f^{\prime}(x)=f(x)-x f^{2}(x)$ với mọi $x \in(0 ;+\infty)$. Biết $f(1)=1$ và $F(1)=\ln 2$. Tính $F(2)$.
Cho hàm số $f(x)$ có nguyên hàm $F(x)$ và thỏa mãn $x f^{\prime}(x)=f(x)-x f^{2}(x)$ với mọi $x \in(0 ;+\infty)$. Biết $f(1)=1$ và $F(1)=\ln 2$. Tính $F(2)$.A. $2 \ln 2$.B. $\ln 5$.C. $3 \ln 2$.D. $2 \ln 3$.
Biết \(\int\limits_0^\pi {\left( {3x + 2} \right){{\cos }^2}x\,{\rm{d}}x} = \frac{a}{b}{\pi ^2} + c\pi \) (với \(a,\,b,\,c\) là các số tự nhiên, \(\frac{a}{b}\) là phân số tối giản). Giá trị của \(a + b + c\)bằng
Biết \(\int\limits_0^\pi {\left( {3x + 2} \right){{\cos }^2}x\,{\rm{d}}x} = \frac{a}{b}{\pi ^2} + c\pi \) (với \(a,\,b,\,c\) là các số tự nhiên, \(\frac{a}{b}\) là phân số tối giản). Giá trị của \(a + b + c\)bằng A. \(6\). B. \(8\). C. \(5\). D. \(4\). Lời giải: Đặt \(I = \int\limits_0^\pi {\left( {3x + 2} \right){{\cos }^2}x\,{\rm{d}}x} […]
Biết tích phân \({\rm{I}} = \int\limits_1^2 {\frac{{\ln {{\left( {2{x^2} + 1} \right)}^x} + 2023x}}{{\ln \left[ {{{\left( {2e{x^2} + e} \right)}^{2{x^2} + 1}}} \right]}}} {\rm{dx = }}\,\,a{\rm{.ln3 + }}\,b{\rm{.ln}}\left( {\frac{{\ln 9e}}{{\ln 3e}}} \right)\) . Với \(a,\,b\, \in \mathbb{Q}\) và \(a,\,b\) là các phân số tối giản. Tính \(P = 8a + 4b\)
Biết tích phân \({\rm{I}} = \int\limits_1^2 {\frac{{\ln {{\left( {2{x^2} + 1} \right)}^x} + 2023x}}{{\ln \left[ {{{\left( {2e{x^2} + e} \right)}^{2{x^2} + 1}}} \right]}}} {\rm{dx = }}\,\,a{\rm{.ln3 + }}\,b{\rm{.ln}}\left( {\frac{{\ln 9e}}{{\ln 3e}}} \right)\) . Với \(a,\,b\, \in \mathbb{Q}\) và \(a,\,b\) là các phân số tối giản. Tính \(P = 8a + 4b\) A. \(P = 1012\) […]
Biết \(f\left( x \right) = \int {{x^3}{e^{{x^2} + 1}}dx} \) và \(f\left( 0 \right) = – \frac{1}{2}e\). Khi đó \(f\left( 1 \right)\) bằng
Biết \(f\left( x \right) = \int {{x^3}{e^{{x^2} + 1}}dx} \) và \(f\left( 0 \right) = – \frac{1}{2}e\). Khi đó \(f\left( 1 \right)\) bằng A. \( – \frac{1}{2}{e^2}\). B. \(\frac{1}{2}e\). C. \(0\). D. \(\frac{1}{2}{e^2}\). Lời giải: Đặt \(t = {x^2} + 1 \Rightarrow dt = 2xdx \Rightarrow xdx = \frac{1}{2}dt\). Lại có \(t = {x^2} + […]