Cho \(F\left( x \right) = \frac{1}{{2{x^2}}}\) là một nguyên hàm của hàm số \(\frac{{f\left( x \right)}}{x}\). Gọi \(G\left( x \right)\) là một nguyên hàm của hàm số \(f’\left( x \right)\ln x\) và \(G\left( 1 \right) = – \frac{1}{2}\). Phương trình \(G\left( {2{x^2} – 1} \right) = m\) có 4 nghiệm phân biệt khi \(m\) thuộc khoảng nào?

Cho \(F\left( x \right) = \frac{1}{{2{x^2}}}\) là một nguyên hàm của hàm số \(\frac{{f\left( x \right)}}{x}\). Gọi \(G\left( x \right)\) là một nguyên hàm của hàm số \(f’\left( x \right)\ln x\) và \(G\left( 1 \right) = – \frac{1}{2}\). Phương trình \(G\left( {2{x^2} – 1} \right) = m\) có 4 nghiệm phân biệt khi \(m\) thuộc khoảng nào?

A. \(\left( {1;2} \right)\).

B. \(\left( {0;1} \right)\).

C. \(\left( { – \frac{1}{2};0} \right)\).

D. \(\left( { – \frac{3}{2}; – 1} \right)\).

Lời giải:

∙ Theo đề bài ta có \(\frac{{f\left( x \right)}}{x} = F’\left( x \right) = {\left( {\frac{1}{{2{x^2}}}} \right)^\prime } = \frac{{ – 1}}{{{x^3}}} \Rightarrow f\left( x \right) = \frac{{ – 1}}{{{x^2}}}\).

Xét \(\int {f’\left( x \right)\ln x{\rm{d}}x} \), đặt \(\left\{ \begin{array}{l}u = \ln x\\{\rm{d}}v = f’\left( x \right){\rm{d}}x\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\rm{d}}u = \frac{1}{x}{\rm{d}}x\\v = f\left( x \right)\end{array} \right.\).

Suy ra \(G\left( x \right) = \int {f’\left( x \right)\ln x{\rm{d}}x} = f\left( x \right)\ln x – \int {\frac{{f\left( x \right)}}{x}{\rm{d}}x = \frac{{ – \ln x}}{{{x^2}}} – \frac{1}{{2{x^2}}} + C} \).

Mà \(G\left( 1 \right) = – \frac{1}{2}\)\( \Rightarrow – \frac{1}{2} + C = – \frac{1}{2} \Leftrightarrow C = 0\)\( \Rightarrow G\left( x \right) = \frac{{ – \ln x}}{{{x^2}}} – \frac{1}{{2{x^2}}} = – \frac{1}{{{x^2}}}\left( {\frac{1}{2} + \ln x} \right)\).

∙ Ta có \(G\left( {2{x^2} – 1} \right) = – \frac{1}{{{{\left( {2{x^2} – 1} \right)}^2}}}.\left[ {\frac{1}{2} + \ln \left( {2{x^2} – 1} \right)} \right]\), tập xác định \(D = \left( { – \infty ; – \frac{{\sqrt 2 }}{2}} \right) \cup \left( {\frac{{\sqrt 2 }}{2}; + \infty } \right)\).

\( \Rightarrow G’\left( {2{x^2} – 1} \right) = \frac{{8x}}{{{{\left( {2{x^2} – 1} \right)}^3}}}.\left[ {\frac{1}{2} + \ln \left( {2{x^2} – 1} \right)} \right] – \frac{{4x}}{{{{\left( {2{x^2} – 1} \right)}^3}}} = \frac{{8x.\ln \left( {2{x^2} – 1} \right)}}{{{{\left( {2{x^2} – 1} \right)}^3}}}\).

\(G’\left( {2{x^2} – 1} \right) = 0 \Rightarrow \ln \left( {2{x^2} – 1} \right) = 0 \Rightarrow 2{x^2} – 1 = 1 \Rightarrow x = \pm 1\).

Bảng biến thiên của \(G\left( {2{x^2} – 1} \right)\) như sau:

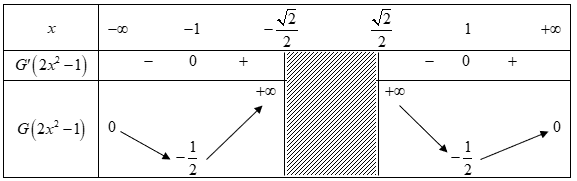
Dựa vào BBT ta thấy phương trình \(G\left( {2{x^2} – 1} \right) = m\) có 4 nghiệm phân biệt khi \(m \in \left( { – \frac{1}{2};0} \right)\).

=========== Đây là các câu ÔN THI TN THPT MÔN TOÁN 2023 – CHUYÊN ĐỀ NGUYÊN HAM – TICH PHÂN – ỨNG DỤNG.