Trắc nghiệm Cực trị của hàm số

Đề toán 2022 [Mức độ 3] Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = \left| {{x^4} – 2m{x^2} + 64x} \right|\) có đúng ba điểm cực trị?

Ngày 01/08/2022 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri ham hop, VDC Toan 2023

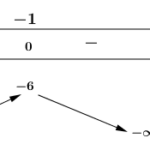
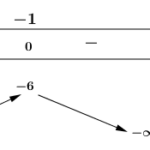
Đề toán 2022 [Mức độ 3] Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = \left| {{x^4} - 2m{x^2} + 64x} \right|\) có đúng ba điểm cực trị? A. \(5\). B. \(6\). C. \(12\). D. \(11\). Lời giải Xét hàm số \(g\left( x \right) = {x^4} - 2m{x^2} + 64x\); \(\mathop {\lim }\limits_{x \to \pm \infty } g\left( x \right) = + \infty \) \(g\left( x … [Đọc thêm...] về

Đề toán 2022 [Mức độ 3] Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = \left| {{x^4} – 2m{x^2} + 64x} \right|\) có đúng ba điểm cực trị?

Đề toán 2022 Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + a.{x^2} – 8x} \right|\) có đúng ba điểm cực trị?

Ngày 01/08/2022 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri ham hop, VDC Toan 2023

Đề toán 2022 Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + a.{x^2} – 8x} \right|\) có đúng ba điểm cực trị?

Ngày 01/08/2022 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri ham hop

Đề toán 2022 Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + a.{x^2} - 8x} \right|\) có đúng ba điểm cực trị? A. \(5\). B. \(6\). C. \(11\). D. \(10\). Lời giải Đặt \(f\left( x \right) = {x^4} + a{x^2} - 8x \Rightarrow f'(x) = 4{x^3} + 2ax - 8.\) \(f'(x) = 0 \Leftrightarrow 4{x^3} + 2ax - 8 = 0 \Leftrightarrow a = \frac{{4 - 2{x^3}}}{x} = … [Đọc thêm...] vềĐề toán 2022 Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + a.{x^2} – 8x} \right|\) có đúng ba điểm cực trị?

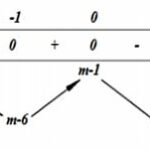
Tập hợp các giá trị của tham số m để hàm số \(y =| 3{x^4} – 4{x^3} – 12{x^2} + m – 1|\) có 7 điểm cực trị là:

Ngày 04/07/2022 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri ham tri tuyet doi, VDC Toan 2023

Câu hỏi: Tập hợp các giá trị của tham số m để hàm số \(y =| 3{x^4} - 4{x^3} - 12{x^2} + m - 1|\) có 7 điểm cực trị là: A. \(\left( {0;6} \right)\) B. \(\left( {6;33} \right)\) C. \(\left( {1;33} \right)\) D. \(\left( {1;6} \right)\) Lời giải tham khảo: Để hàm số \(y = \left| {3{x^4} - 4{x^3} - … [Đọc thêm...] vềTập hợp các giá trị của tham số m để hàm số \(y =| 3{x^4} – 4{x^3} – 12{x^2} + m – 1|\) có 7 điểm cực trị là:

Cho hàm số \(y = f\left( x \right) = \dfrac{1}{3}{x^3} – \left( {m + 1} \right){x^2} + \left( {m + 3} \right)x + m – 4\). Tìm để hàm số \(y = f\left( {\left| x \right|} \right)\) có 5 điểm cực trị?

Ngày 04/07/2022 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri ham tri tuyet doi, VDC Toan 2022, VDC Toan 2023

Câu hỏi: Cho hàm số \(y = f\left( x \right) = \dfrac{1}{3}{x^3} - \left( {m + 1} \right){x^2} + \left( {m + 3} \right)x + m - 4\). Tìm để hàm số \(y = f\left( {\left| x \right|} \right)\) có 5 điểm cực trị? A. \( - 3 < m < 1\) B. \(m > 1\) C. \(m > 4\) D. \(m > 0\) Lời giải tham khảo: Đồ thị hàm số \(y = … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right) = \dfrac{1}{3}{x^3} – \left( {m + 1} \right){x^2} + \left( {m + 3} \right)x + m – 4\). Tìm để hàm số \(y = f\left( {\left| x \right|} \right)\) có 5 điểm cực trị?

Biết \({m_0}\) là giá trị của tham số m để hàm số \(y = {x^3} – 3{x^2} + mx – 1\) có hai điểm cực trị \({x_1},\,\,{x_2}\) sao cho \(x_1^2 + x_2^2 – {x_1}{x_2} = 13\). Mệnh đề nào dưới đây đúng?

Ngày 04/07/2022 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cực trị - Đúng - sai

Câu hỏi: Biết \({m_0}\) là giá trị của tham số m để hàm số \(y = {x^3} - 3{x^2} + mx - 1\) có hai điểm cực trị \({x_1},\,\,{x_2}\) sao cho \(x_1^2 + x_2^2 - {x_1}{x_2} = 13\). Mệnh đề nào dưới đây đúng? A. \({m_0} \in \left( { - 1;7} \right)\) B. \({m_0} \in \left( { - 15; - 7} \right)\) C. \({m_0} \in \left( {7;10} … [Đọc thêm...] vềBiết \({m_0}\) là giá trị của tham số m để hàm số \(y = {x^3} – 3{x^2} + mx – 1\) có hai điểm cực trị \({x_1},\,\,{x_2}\) sao cho \(x_1^2 + x_2^2 – {x_1}{x_2} = 13\). Mệnh đề nào dưới đây đúng?

Cho hàm số \(y=f(x)\) có đạo hàm là \(f'(x)=x^2+10 x, \forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=f\left(x^4-8 x^2+m\right)\) có đúng 9 điểm cực trị?

Ngày 15/05/2022 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri ham hop, VDC Toan 2022

Câu 50: Đề tham khảo 2022 Cho hàm số \(y=f(x)\) có đạo hàm là \(f'(x)=x^2+10 x, \forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=f\left(x^4-8 x^2+m\right)\) có đúng 9 điểm cực trị? A. 16 B. 9 C. 15 D. 10 LỜI GIẢI Ta có \(f'(x)=0\Leftrightarrow … [Đọc thêm...] vềCho hàm số \(y=f(x)\) có đạo hàm là \(f'(x)=x^2+10 x, \forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=f\left(x^4-8 x^2+m\right)\) có đúng 9 điểm cực trị?

Chứng minh rằng hàm số \(y = {x^4} – 6{x^2} + 4x + 6\) luôn luôn có 3 cực trị đồng thời gốc toạ độ O là trọng tâm của tam giác tạo bởi 3 đỉnh là 3 điểm cực trị của đồ thị hàm số.

Ngày 09/10/2021 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số, Bài tập Hàm số Tag với:Bai Toan hay 2022, Cực trị của hàm số, Cuc tri VDC - Trả lời ngắn

Xét hàm số \(y = {x^4} - 6{x^2} + 4x + 6\). Tập xác định: \(D = \mathbb{R}\). Ta có \(y' = 4{x^3} - 12x + 4\)\( = 4\left( {{x^3} - 3x + 1} \right)\) ; \(y' = 0\)\( \Leftrightarrow {x^3} - 3x + 1 = 0\). Xét hàm số \(g\left( x \right) = {x^3} - 3x + 1\). Tập xác định: \(D = \mathbb{R}\). \(g'\left( x \right) = 3{x^2} - 3\), \(g'\left( x \right) = 0 … [Đọc thêm...] vềChứng minh rằng hàm số \(y = {x^4} – 6{x^2} + 4x + 6\) luôn luôn có 3 cực trị đồng thời gốc toạ độ O là trọng tâm của tam giác tạo bởi 3 đỉnh là 3 điểm cực trị của đồ thị hàm số.

Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới đây.
Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^3} + 3{x^2} – 4} \right)\) là

Ngày 16/09/2021 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Trắc nghiệm cực trị Vận dụng

Câu hỏi: Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới đây. Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^3} + 3{x^2} - 4} \right)\) là A. \(6.\) B. \(9.\) C. \(7.\) D. \(12.\) LỜI GIẢI CHI TIẾT Fb: Võ Đức Toàn Ta có \(g'(x) = (3{x^2} + 6x).f'\left( {{x^3} + 3{x^2} - 4} \right)\). \(g'(x) = 0 … [Đọc thêm...] vềCho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới đây.