Trắc nghiệm Cực trị của hàm số

Cho hàm số $y = f(x) =\dfrac{ax^2 + bx + c}{dx + e}$ có đồ thị như hình bên. Điểm cực tiểu của đồ thị hàm số là

Ngày 01/11/2025 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cực trị của hàm số

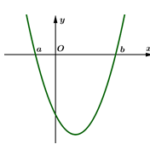
Câu 3. Cho hàm số $y = f(x) =\dfrac{ax^2 + bx + c}{dx + e}$ có đồ thị như hình bên. Điểm cực tiểu của đồ thị hàm số làA. $x = -1$.B. $\left(3;-3\right)$.C. $\left(-1;-\dfrac{1}{3}\right)$.D. $x = 3$.Lời giải: Dựa vào đồ thị ta có điểm cực tiểu của đồ thị hàm số là $\left(-1;-\dfrac{1}{3}\right)$. … [Đọc thêm...] vềCho hàm số $y = f(x) =\dfrac{ax^2 + bx + c}{dx + e}$ có đồ thị như hình bên. Điểm cực tiểu của đồ thị hàm số là

Cho hàm số $y=f(x)$ có bảng biến thiên như bên dưới. Đồ thị hàm số đạt cực đại tại điểm nào sau đây?

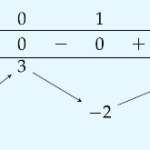
Ngày 01/11/2025 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cực trị của hàm số

Câu 2. Cho hàm số $y=f(x)$ có bảng biến thiên như bên dưới. Đồ thị hàm số đạt cực đại tại điểm nào sau đây?A. $x = \dfrac{5}{3}$.B. $\left(\dfrac{5}{3}; -\dfrac{31}{27}\right)$.C. $x = 1$.D. $\left(1; -1\right)$.Lời giải: Dựa vào bảng biến thiên ta kết luận đồ thị hàm số đạt cực đại tại điểm $\left(1; -1\right)$ … [Đọc thêm...] vềCho hàm số $y=f(x)$ có bảng biến thiên như bên dưới. Đồ thị hàm số đạt cực đại tại điểm nào sau đây?

Hàm số nào dưới đây không có cực trị ?

Ngày 01/11/2025 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cực trị của hàm số

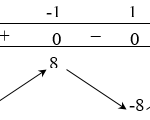
Câu hỏi Hàm số nào dưới đây không có cực trị?A. $y=3 x^{4} - 6 x^{2} - 8$.B. $y=\dfrac{x^{2} + 4 x + 5}{4 x - 6}$.C. $y=\dfrac{x^{3}}{3} + \dfrac{9 x^{2}}{2} + 18 x + 1$.D. $y=\dfrac{3 x - 4}{4 x + 1}$.Lời giải: Ta thấy hàm số $y=\dfrac{3 x - 4}{4 x + 1}$ không có cực trị. … [Đọc thêm...] vềHàm số nào dưới đây không có cực trị ?

Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ $mg/l$ của thuốc trong máu sau $x$ phút (kể từ khi bắt đầu tiêm)

Ngày 01/11/2025 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:CUC TRI HAM SO VDC

Câu 8. Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ $mg/l$ của thuốc trong máu sau $x$ phút (kể từ khi bắt đầu tiêm) được xác định bởi công thức: $C(x)=\dfrac{30x}{{{x}^{2}}+2}$.Để đưa ra những lời khuyên và cách xử lí phù hợp cho bệnh nhân, ta cần tìm khoảng thời gian mà nồng độ của thuốc trong máu đang tăng. Em hãy cho biết hàm nồng độ thuốc trong máu $C(x)$ đạt giá trị … [Đọc thêm...] vềKhi loại thuốc A được tiêm vào bệnh nhân, nồng độ $mg/l$ của thuốc trong máu sau $x$ phút (kể từ khi bắt đầu tiêm)

Biết đồ thị hàm số $y=\frac{1}{4} x^{4}-(3 m+1) x^{2}+2(m+1)$ có ba điểm cực trị $A, B, C$ sao cho $\triangle A B C$ nhận gốc tọa độ $O$ làm trọng tâm. Mệnh đề nào dưới đây đúng?

Ngày 13/12/2023 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri VDC - Trả lời ngắn, VDC Toan 2023

Biết đồ thị hàm số $y=\frac{1}{4} x^{4}-(3 m+1) x^{2}+2(m+1)$ có ba điểm cực trị $A, B, C$ sao cho $\triangle A B C$ nhận gốc tọa độ $O$ làm trọng tâm. Mệnh đề nào dưới đây đúng? A. $m=\frac{1}{3}$. B. $m=-\frac{2}{3}$. C. $m=1$. D. $m=0$. Ta có $y^{\prime}=x^{3}-2(3 m+1) x=x\left(x^{2}-6 m-2\right)=0 \Leftrightarrow\left[\begin{array}{l}x=0 \\ x^{2}=6 m+2 … [Đọc thêm...] vềBiết đồ thị hàm số $y=\frac{1}{4} x^{4}-(3 m+1) x^{2}+2(m+1)$ có ba điểm cực trị $A, B, C$ sao cho $\triangle A B C$ nhận gốc tọa độ $O$ làm trọng tâm. Mệnh đề nào dưới đây đúng?

Cho hàm số $y=\frac{1}{3} m x^{3}-(m-1) x^{2}+3(m-2) x+2023$ với $m$ là tham số. Tìm m để hàm số có 2 cực trị

Ngày 13/12/2023 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri VDC - Trả lời ngắn, VDC Toan 2023

Cho hàm số $y=\frac{1}{3} m x^{3}-(m-1) x^{2}+3(m-2) x+2023$ với $m$ là tham số. Tổng bình phương tất cả các giá trị của $m$ để hàm số có hai điểm cực trị $x_{1}, x_{2}$ thỏa mãn $x_{1}+2 x_{2}=1$ bằng A. $\frac{25}{4}$. B. $\frac{22}{9}$. C. $\frac{8}{3}$. D. $\frac{40}{9}$. LỜI GIẢI Ta có $y^{\prime}=m x^{2}-2(m-1) x+3(m-2)$. Để hàm số có hai điểm cực trị $x_{1}, x_{2}$ … [Đọc thêm...] vềCho hàm số $y=\frac{1}{3} m x^{3}-(m-1) x^{2}+3(m-2) x+2023$ với $m$ là tham số. Tìm m để hàm số có 2 cực trị

Biết $f(-1)=1$, hàm số $y=\left|f\left(x^{2}-2 x\right)\right|$ có bao nhiêu điểm cực trị? Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

Ngày 30/05/2023 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri ham hop, VDC Toan 2023

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau: Biết $f(-1)=1$, hàm số $y=\left|f\left(x^{2}-2 x\right)\right|$ có bao nhiêu điểm cực trị?A. 11.B. 9 .C. 15 .D. 7 . … [Đọc thêm...] vềBiết $f(-1)=1$, hàm số $y=\left|f\left(x^{2}-2 x\right)\right|$ có bao nhiêu điểm cực trị? Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y = – {x^4} + 6{x^2} + mx$ có ba điểm cực trị?

Ngày 13/03/2023 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Trắc nghiệm cực trị Vận dụng

Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y = - {x^4} + 6{x^2} + mx$ có ba điểm cực trị? A. $17$ . B. $15$ . C. $3$ . D. $7$ . Lời giải: Chọn B Ta có: $y' = - 4{x^3} + 12x + m$ . Xét phương trình $y' = 0 \Leftrightarrow - 4{x^3} + 12x + m = … [Đọc thêm...] vềCó bao nhiêu giá trị nguyên của tham số \(m$ để hàm số $y = – {x^4} + 6{x^2} + mx$ có ba điểm cực trị?

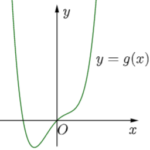
Cho hàm số bậc ba y=f(x) có đồ thị của hàm đạo hàm f'(x) như hình vẽ và f(b)=1. Số giá trị nguyên của $m \in [-5;5]$ để hàm số $g\left(x\right)=\left|f^2\left(x\right)+4f\left(x\right)+m\right|$ có đúng 5 điểm cực trị là

Ngày 19/12/2022 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri ham tri tuyet doi, VDC Toan 2023

Cho hàm số bậc ba y=f(x) có đồ thị của hàm đạo hàm f'(x) như hình vẽ và f(b)=1. Số giá trị nguyên của $m\in[-5;5]$ để hàm số $g\left(x\right)=\left|f^2\left(x\right)+4f\left(x\right)+m\right|$ có đúng 5 điểm cực trị là A. $8$. B. $10$. C. $9$. D. $7$. LỜI GIẢI Theo bài ra ta có bảng biến thiên của hàm số $y = f\left( x \right)$ như sau: Đặt … [Đọc thêm...] vềCho hàm số bậc ba y=f(x) có đồ thị của hàm đạo hàm f'(x) như hình vẽ và f(b)=1. Số giá trị nguyên của $m \in [-5;5]$ để hàm số $g\left(x\right)=\left|f^2\left(x\right)+4f\left(x\right)+m\right|$ có đúng 5 điểm cực trị là

Đề toán 2022 [2D1-2.7-4] Có bao nhiêu giá trị nguyên âm của tham số $a$ để hàm số $y = \left| {{x^4} + 2a{x^2} + 8x} \right|$ có đúng ba điểm cực trị.

Ngày 01/08/2022 Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:Cuc tri ham hop, TN THPT 2022, VDC Toan 2023

Đề toán 2022 [2D1-2.7-4] Có bao nhiêu giá trị nguyên âm của tham số $a$ để hàm số $y = \left| {{x^4} + 2a{x^2} + 8x} \right|$ có đúng ba điểm cực trị. A. $2$. B. $6$. C.$5$. D. $3$. Lời giải Xét hàm số $g\left( x \right) = {x^4} + 2a{x^2} + 8x$; $\mathop {\lim }\limits_{x \to \pm \infty } \,g\left( x \right) = + \infty $. \(g\left( x … [Đọc thêm...] về

Đề toán 2022 [2D1-2.7-4] Có bao nhiêu giá trị nguyên âm của tham số $a$ để hàm số $y = \left| {{x^4} + 2a{x^2} + 8x} \right|$ có đúng ba điểm cực trị.

Cho hàm số $y = f(x) =\dfrac{ax^2 + bx + c}{dx + e}$ có đồ thị như hình bên. Điểm cực tiểu của đồ thị hàm số là

Cho hàm số $y=f(x)$ có bảng biến thiên như bên dưới. Đồ thị hàm số đạt cực đại tại điểm nào sau đây?

Hàm số nào dưới đây không có cực trị ?

Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ $mg/l$ của thuốc trong máu sau $x$ phút (kể từ khi bắt đầu tiêm)

Biết đồ thị hàm số $y=\frac{1}{4} x^{4}-(3 m+1) x^{2}+2(m+1)$ có ba điểm cực trị $A, B, C$ sao cho $\triangle A B C$ nhận gốc tọa độ $O$ làm trọng tâm. Mệnh đề nào dưới đây đúng?

Cho hàm số $y=\frac{1}{3} m x^{3}-(m-1) x^{2}+3(m-2) x+2023$ với $m$ là tham số. Tìm m để hàm số có 2 cực trị

Biết $f(-1)=1$, hàm số $y=\left|f\left(x^{2}-2 x\right)\right|$ có bao nhiêu điểm cực trị? Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = – {x^4} + 6{x^2} + mx\) có ba điểm cực trị?

Cho hàm số bậc ba y=f(x) có đồ thị của hàm đạo hàm f'(x) như hình vẽ và f(b)=1. Số giá trị nguyên của \(m \in [-5;5]\) để hàm số \(g\left(x\right)=\left|f^2\left(x\right)+4f\left(x\right)+m\right|\) có đúng 5 điểm cực trị là

Đề toán 2022 [2D1-2.7-4] Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + 2a{x^2} + 8x} \right|\) có đúng ba điểm cực trị.