Câu 8. Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ $mg/l$ của thuốc trong máu sau $x$ phút (kể từ khi bắt đầu tiêm) được xác định bởi công thức: $C(x)=\dfrac{30x}{{{x}^{2}}+2}$.Để đưa ra những lời khuyên và cách xử lí phù hợp cho bệnh nhân, ta cần tìm khoảng thời gian mà nồng độ của thuốc trong máu đang tăng. Em hãy cho biết hàm nồng độ thuốc trong máu $C(x)$ đạt giá trị … [Đọc thêm...] vềKhi loại thuốc A được tiêm vào bệnh nhân, nồng độ $mg/l$ của thuốc trong máu sau $x$ phút (kể từ khi bắt đầu tiêm)
CUC TRI HAM SO VDC
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\), có đạo hàm \(f’\left( x \right) = \left( {{x^2} – 9} \right)\left( {x – 5} \right).\) Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số \(g\left( x \right) = f\left( {{e^{{x^3} + 3{x^2}}} – m} \right)\) có đúng \(7\) điểm cực trị
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\), có đạo hàm \(f'\left( x \right) = \left( {{x^2} - 9} \right)\left( {x - 5} \right).\) Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số \(g\left( x \right) = f\left( {{e^{{x^3} + 3{x^2}}} - m} \right)\) có đúng \(7\) điểm cực trị A. \(3\) B. \(4\) C. \(5\) D. \(6\) Lời giải: Ta có \(g'\left( x … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\), có đạo hàm \(f’\left( x \right) = \left( {{x^2} – 9} \right)\left( {x – 5} \right).\) Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số \(g\left( x \right) = f\left( {{e^{{x^3} + 3{x^2}}} – m} \right)\) có đúng \(7\) điểm cực trị
[Mức độ 4] Cho hàm số đa thức \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Biết rằng \(f\left( 0 \right) = 0\), \(f\left( { – 3} \right) = f\left( {\frac{3}{2}} \right) = – \frac{{19}}{4}\) và đồ thị hàm số \(y = f’\left( x \right)\) có dạng như hình vẽ.
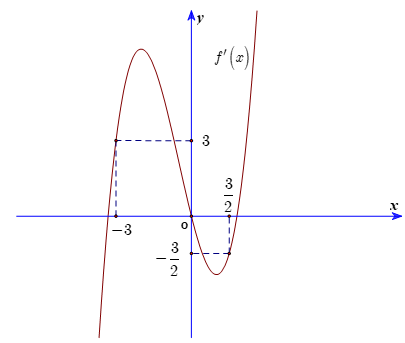
Hàm số \(g\left( x \right) = \left| {4f\left( x \right) + 2{x^2}} \right|\) giá trị lớn nhất của \(g\left( x \right)\) trên \(\left[ { – 2;\frac{3}{2}} \right]\) là
[Mức độ 4] Cho hàm số đa thức \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Biết rằng \(f\left( 0 \right) = 0\), \(f\left( { - 3} \right) = f\left( {\frac{3}{2}} \right) = - \frac{{19}}{4}\) và đồ thị hàm số \(y = f'\left( x \right)\) có dạng như hình vẽ. Hàm số \(g\left( x \right) = \left| {4f\left( x \right) + 2{x^2}} \right|\) giá trị lớn nhất của \(g\left( … [Đọc thêm...] về[Mức độ 4] Cho hàm số đa thức \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Biết rằng \(f\left( 0 \right) = 0\), \(f\left( { – 3} \right) = f\left( {\frac{3}{2}} \right) = – \frac{{19}}{4}\) và đồ thị hàm số \(y = f’\left( x \right)\) có dạng như hình vẽ.
Hàm số \(g\left( x \right) = \left| {4f\left( x \right) + 2{x^2}} \right|\) giá trị lớn nhất của \(g\left( x \right)\) trên \(\left[ { – 2;\frac{3}{2}} \right]\) là
[ Mức độ 4 ] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {\left( {x + 1} \right)^2}\left( {{x^2} – 2x} \right)\) với \(\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(f\left( {{x^2} – 4x + m} \right)\) có \(5\) điểm cực trị?
[ Mức độ 4 ] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x + 1} \right)^2}\left( {{x^2} - 2x} \right)\) với \(\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(f\left( {{x^2} - 4x + m} \right)\) có \(5\) điểm cực trị? A.\(8.\) B. \(7.\) C. \(6.\) D. \(5.\) Lời giải: Đặt \(g\left( x … [Đọc thêm...] về[ Mức độ 4 ] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {\left( {x + 1} \right)^2}\left( {{x^2} – 2x} \right)\) với \(\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(f\left( {{x^2} – 4x + m} \right)\) có \(5\) điểm cực trị?
[Mức độ 3] Cho hàm số \(y\, = \,f(x)\,\) có đạo hàm và liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( { – 6} \right) = 42\) và bảng xét dấu đạo hàm như

Giá trị nhỏ nhất của hàm số \(y\, = \,f\left( { – \,3{x^4}\,\, + \,\,12{x^2}\, – \,15} \right)\, + \,2{x^6}\, + \,6{x^4}\, – 48{x^2}\) trên đoạn \(\left[ { – 1;1} \right]\) bằng
[Mức độ 3] Cho hàm số \(y\, = \,f(x)\,\) có đạo hàm và liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( { - 6} \right) = 42\) và bảng xét dấu đạo hàm như Giá trị nhỏ nhất của hàm số \(y\, = \,f\left( { - \,3{x^4}\,\, + \,\,12{x^2}\, - \,15} \right)\, + \,2{x^6}\, + \,6{x^4}\, - 48{x^2}\) trên đoạn \(\left[ { - 1;1} \right]\) bằng A. 3. B. 0. C. 1. D. 2. Lời … [Đọc thêm...] về[Mức độ 3] Cho hàm số \(y\, = \,f(x)\,\) có đạo hàm và liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( { – 6} \right) = 42\) và bảng xét dấu đạo hàm như
Giá trị nhỏ nhất của hàm số \(y\, = \,f\left( { – \,3{x^4}\,\, + \,\,12{x^2}\, – \,15} \right)\, + \,2{x^6}\, + \,6{x^4}\, – 48{x^2}\) trên đoạn \(\left[ { – 1;1} \right]\) bằng
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} + x – 6\) với mọi \(x \in \mathbb{R}\). Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} – 3{x^2} – 9x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0;4} \right)\). Tính tổng các phần tử của \(S\).
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2} + x - 6\) với mọi \(x \in \mathbb{R}\). Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} - 3{x^2} - 9x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0;4} \right)\). Tính tổng các phần tử của … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} + x – 6\) với mọi \(x \in \mathbb{R}\). Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} – 3{x^2} – 9x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0;4} \right)\). Tính tổng các phần tử của \(S\).
[Mức độ 3] Cho hàm số \(f(x) = {x^5} + 3{x^3} – 4\;m\). Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt[3]{{f(x) + m}}} \right) = {x^3} – m\) có nghiệm thuộc \(\left[ {1;2} \right]\)?
[Mức độ 3] Cho hàm số \(f(x) = {x^5} + 3{x^3} - 4\;m\). Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt[3]{{f(x) + m}}} \right) = {x^3} - m\) có nghiệm thuộc \(\left[ {1;2} \right]\)? A. \(15\). B. \(16\). C. \(17\). D. \(18\). Lời giải: Đặt \({\rm{ }}\sqrt[3]{{f(x) + m}} = u \Rightarrow f(x) + m = {u^3} \Rightarrow \left\{ … [Đọc thêm...] về[Mức độ 3] Cho hàm số \(f(x) = {x^5} + 3{x^3} – 4\;m\). Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt[3]{{f(x) + m}}} \right) = {x^3} – m\) có nghiệm thuộc \(\left[ {1;2} \right]\)?
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} – 5x – 6\,,\,\forall x \in \mathbb{R}\). Tính tổng tất cả các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( { – {x^3} + 3x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0\,;\,3} \right)\).
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2} - 5x - 6\,,\,\forall x \in \mathbb{R}\). Tính tổng tất cả các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( { - {x^3} + 3x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0\,;\,3} \right)\). A. \(119\) . B. \(120\) … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} – 5x – 6\,,\,\forall x \in \mathbb{R}\). Tính tổng tất cả các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( { – {x^3} + 3x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0\,;\,3} \right)\).
[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị
\(y = f’\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x – m} \right) – \frac{1}{2}{\left( {x – m – 1} \right)^2} + 2022\), với \(m\) là tham số thự
C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {2;3} \right)\). Tổng tất cả các phần tử trong \(S\) bằng
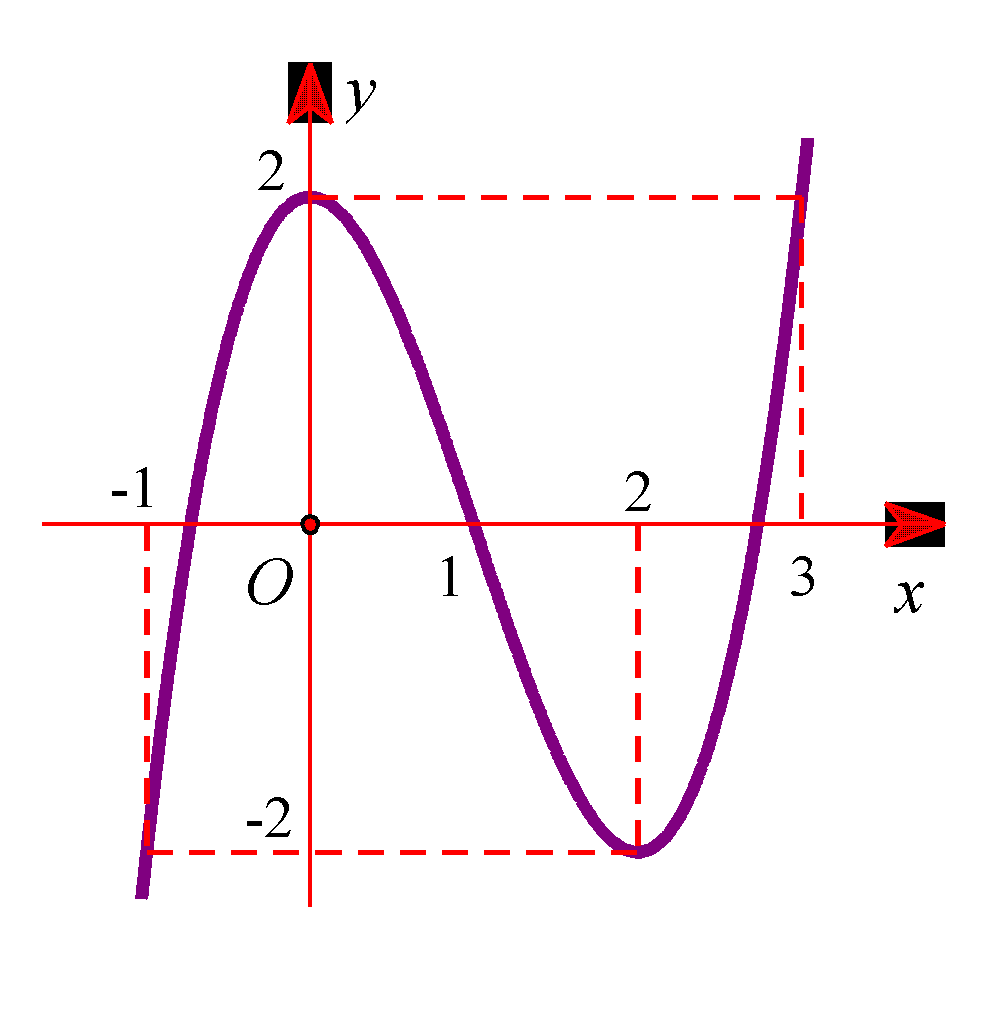
[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị \(y = f'\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x - m} \right) - \frac{1}{2}{\left( {x - m - 1} \right)^2} + 2022\), với \(m\) là tham số thự C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng … [Đọc thêm...] về[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị
\(y = f’\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x – m} \right) – \frac{1}{2}{\left( {x – m – 1} \right)^2} + 2022\), với \(m\) là tham số thự
C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {2;3} \right)\). Tổng tất cả các phần tử trong \(S\) bằng
[Mức độ 4] Cho hàm số bậc ba \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{\left( {{x^2} – 3x + 2} \right)\sqrt {2x + 1} }}{{\left( {{x^4} – 5{x^2} + 4} \right).f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?
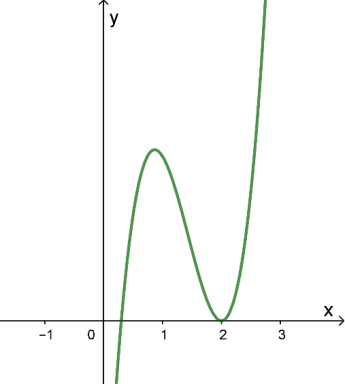
[Mức độ 4] Cho hàm số bậc ba \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{\left( {{x^2} - 3x + 2} \right)\sqrt {2x + 1} }}{{\left( {{x^4} - 5{x^2} + 4} \right).f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng? A. 4. B. 3. C. 2. D. 6. Lời giải: Quan sát đồ thị hàm số … [Đọc thêm...] về[Mức độ 4] Cho hàm số bậc ba \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{\left( {{x^2} – 3x + 2} \right)\sqrt {2x + 1} }}{{\left( {{x^4} – 5{x^2} + 4} \right).f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?
