Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = – {x^4} + 6{x^2} + mx\) có ba điểm cực trị?

A. \(17\) .

 B. \(15\) .

 C. \(3\) .

 D. \(7\) .

Lời giải:

Chọn B

Ta có: \(y’ =  – 4{x^3} + 12x + m\) . Xét phương trình \(y’ = 0 \Leftrightarrow  – 4{x^3} + 12x + m = 0\,\,\,\,\,\,\left( 1 \right)\) .

Để hàm số có ba điểm cực trị thì phương trình \(\left( 1 \right)\) phải có 3 nghiệm phân biệt.

Ta có: \(\left( 1 \right) \Leftrightarrow m = 4{x^3} – 12x\) .

Xét hàm số \(g\left( x \right) = 4{x^3} – 12x\) có \(g’\left( x \right) = 12{x^2} – 12\) . Cho \(g’\left( x \right) = 0 \Leftrightarrow 12{x^2} – 12 = 0 \Leftrightarrow x =  \pm 1\) .

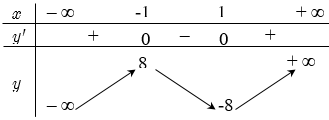
Bảng biến thiên của \(g\left( x \right)\)

\(m\) để hàm số \(y = – {x^4} + 6{x^2} + mx\) có ba điểm cực trị?” title=”Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = – {x^4} + 6{x^2} + mx\) có ba điểm cực trị?” />

Dựa vào bảng biến thiên ta thấy, phương trình \(\left( 1 \right)\) có 3 nghiệm phân biệt khi \( – 8 < m < 8\) .

Do \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { – 7, – 6, – 5,…,5,6,7} \right\}\) .

Vậy có 15 giá trị nguyên của tham số \(m\) thỏa yêu cầu đề bài.