Đề bài: Cho hình chóp $S.ABC$, trong đó $SA$ vuông góc với mặt đáy $ABC$. Đáy là tam giác cân tại $A$, đồ dài trung tuyên $AD=a, $; cạnh bên $SB$ tạo với mặt đáy một góc $\alpha$ và tạo với mặt phẳng $(SAD)$ góc $\beta$. Tìm thể tích hình chóp $S.ABC$. Lời giải Cần giải chi tiết ( đáp án: $\frac{a^3\sin \alpha \sin \beta}{3\cos (\alpha+\beta)\cos(\alpha-\beta)}$.) … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$, trong đó $SA$ vuông góc với mặt đáy $ABC$. Đáy là tam giác cân tại $A$, đồ dài trung tuyên $AD=a, $; cạnh bên $SB$ tạo với mặt đáy một góc $\alpha$ và tạo với mặt phẳng $(SAD)$ góc $\beta$. Tìm thể tích hình chóp $S.ABC$.
Hình học không gian
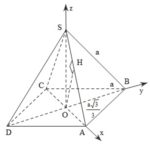
Đề bài: Gọi $O$ là tâm hình thoi $ABCD$ cạnh $a$ với $OB=\frac{a\sqrt{3} }{3} $. Trên đường thẳng vuông góc với mặt phẳng $(ABCD)$ tại $O$ lấy điểm $S$ với $SB=a$a) Chứng minh rằng tam giác $SAC$ vuông và $SC\bot BD$b) Tính góc phẳng nhị diện cạnh $SA$ và tính khoảng cách giữa $SA$ và $BD$
Đề bài: Gọi $O$ là tâm hình thoi $ABCD$ cạnh $a$ với $OB=\frac{a\sqrt{3} }{3} $. Trên đường thẳng vuông góc với mặt phẳng $(ABCD)$ tại $O$ lấy điểm $S$ với $SB=a$a) Chứng minh rằng tam giác $SAC$ vuông và $SC\bot BD$b) Tính góc phẳng nhị diện cạnh $SA$ và tính khoảng cách giữa $SA$ và $BD$ Lời giải a) Ta có: $OA=\sqrt{AB^2-OB^2}=\sqrt{a^2-\frac{a^2}{3} … [Đọc thêm...] vềĐề bài: Gọi $O$ là tâm hình thoi $ABCD$ cạnh $a$ với $OB=\frac{a\sqrt{3} }{3} $. Trên đường thẳng vuông góc với mặt phẳng $(ABCD)$ tại $O$ lấy điểm $S$ với $SB=a$a) Chứng minh rằng tam giác $SAC$ vuông và $SC\bot BD$b) Tính góc phẳng nhị diện cạnh $SA$ và tính khoảng cách giữa $SA$ và $BD$
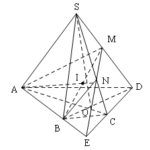
Đề bài: Cho hình chóp tứ giác $S.ABCD$ ($AB$ không song song với $CD$) giao tuyến của $AC,BD$ là điểm $O,M$ là một điểm di chuyển trên cạnh $SD$.Mặt phẳng $(ABM)$ cắt cạnh $SC$ tại $N$$a.$ Chứng minh khi $M$ di chuyển trên $SD$ thì đường thẳng $MN$ luôn đi qua một điểm cố định.$b.$ Gọi $I$ là giao điểm của $AN,BM$.Chứng minh ba điểm $S,I,O$ thẳng hàng$c.$ Gọi $J$ là giao điểm của $AM,BN$.Chứng minh khi $M$ di chuyển trên $SD$ thì $J$ di chuyển trên một đường thẳng cố định
Đề bài: Cho hình chóp tứ giác $S.ABCD$ ($AB$ không song song với $CD$) giao tuyến của $AC,BD$ là điểm $O,M$ là một điểm di chuyển trên cạnh $SD$.Mặt phẳng $(ABM)$ cắt cạnh $SC$ tại $N$$a.$ Chứng minh khi $M$ di chuyển trên $SD$ thì đường thẳng $MN$ luôn đi qua một điểm cố định.$b.$ Gọi $I$ là giao điểm của $AN,BM$.Chứng minh ba điểm $S,I,O$ thẳng hàng$c.$ Gọi $J$ là giao điểm … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác $S.ABCD$ ($AB$ không song song với $CD$) giao tuyến của $AC,BD$ là điểm $O,M$ là một điểm di chuyển trên cạnh $SD$.Mặt phẳng $(ABM)$ cắt cạnh $SC$ tại $N$$a.$ Chứng minh khi $M$ di chuyển trên $SD$ thì đường thẳng $MN$ luôn đi qua một điểm cố định.$b.$ Gọi $I$ là giao điểm của $AN,BM$.Chứng minh ba điểm $S,I,O$ thẳng hàng$c.$ Gọi $J$ là giao điểm của $AM,BN$.Chứng minh khi $M$ di chuyển trên $SD$ thì $J$ di chuyển trên một đường thẳng cố định
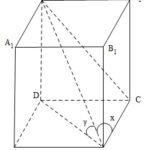
Đề bài: Một lăng trụ tứ giác đều có cạnh đáy $a$, đường chéo của lăng trụ tạo với cạnh bên và với đường chéo đáy hai góc có tổng bằng $135^0$. Xác định đường cao lăng trụ.
Đề bài: Một lăng trụ tứ giác đều có cạnh đáy $a$, đường chéo của lăng trụ tạo với cạnh bên và với đường chéo đáy hai góc có tổng bằng $135^0$. Xác định đường cao lăng trụ. Lời giải Kí hiệu góc giữa đường chéo $D_1B$ và đường chéo đáy $DB$ là $y$ và góc giữa $D_1B$ và $BC$ là $x$, theo giả thiết $x+y=135^0$Ta có $\left. {\begin{array}{*{20}{c}}BC=\cos … [Đọc thêm...] vềĐề bài: Một lăng trụ tứ giác đều có cạnh đáy $a$, đường chéo của lăng trụ tạo với cạnh bên và với đường chéo đáy hai góc có tổng bằng $135^0$. Xác định đường cao lăng trụ.
Đề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình vuông cạnh $a$. Hai mặt bên $(SAB),(SAD)$ cùng vuông góc với đáy, $SA=a$. Tìm bán kính hình cầu nội tiếp hình chóp.
Đề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình vuông cạnh $a$. Hai mặt bên $(SAB),(SAD)$ cùng vuông góc với đáy, $SA=a$. Tìm bán kính hình cầu nội tiếp hình chóp. Lời giải … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình vuông cạnh $a$. Hai mặt bên $(SAB),(SAD)$ cùng vuông góc với đáy, $SA=a$. Tìm bán kính hình cầu nội tiếp hình chóp.
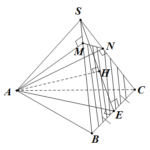
Đề bài: Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh bằng $a. SA=2a$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Gọi $M,N$ tương ứng là hình chiếu vuông góc của $A$ trên $SB,SC$. Tìm thể tích khối chóp $A.BMNC$.
Đề bài: Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh bằng $a. SA=2a$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Gọi $M,N$ tương ứng là hình chiếu vuông góc của $A$ trên $SB,SC$. Tìm thể tích khối chóp $A.BMNC$. Lời giải Ta có thể tích $V_{A.BMNC}=V_{S.ABC}-V_{S.AMN} (1)$Theo bài toán cơ bản thì $\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SM}{SB}.\frac{SN}{SC}$Vì … [Đọc thêm...] vềĐề bài: Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh bằng $a. SA=2a$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Gọi $M,N$ tương ứng là hình chiếu vuông góc của $A$ trên $SB,SC$. Tìm thể tích khối chóp $A.BMNC$.
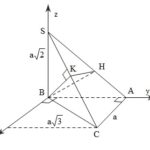
Đề bài: Cho tứ diện $SABC, \Delta ABC$ vuông tại $A$ có $AC=a, BC=a\sqrt{3}, SB=a\sqrt{2}, SB\bot (ABC) $. Qua $B$ vẽ $BH\bot SA, BK\bot SC (H\in SA, K\in SC)$ a) Chứng minh $SC\bot (BHK)$b) Tính diện tích $\Delta BHK$c) Tính $[A,SC,B]$
Đề bài: Cho tứ diện $SABC, \Delta ABC$ vuông tại $A$ có $AC=a, BC=a\sqrt{3}, SB=a\sqrt{2}, SB\bot (ABC) $. Qua $B$ vẽ $BH\bot SA, BK\bot SC (H\in SA, K\in SC)$ a) Chứng minh $SC\bot (BHK)$b) Tính diện tích $\Delta BHK$c) Tính $[A,SC,B]$ Lời giải Trong $(ABC)$, vẽ $Bx\bot BA$Ta có: $AB=\sqrt{BC^2-AC^2} =a\sqrt{2} $$\Rightarrow \Delta BAS$ vuông cân tại … [Đọc thêm...] vềĐề bài: Cho tứ diện $SABC, \Delta ABC$ vuông tại $A$ có $AC=a, BC=a\sqrt{3}, SB=a\sqrt{2}, SB\bot (ABC) $. Qua $B$ vẽ $BH\bot SA, BK\bot SC (H\in SA, K\in SC)$ a) Chứng minh $SC\bot (BHK)$b) Tính diện tích $\Delta BHK$c) Tính $[A,SC,B]$
Đề bài: Cho tứ diện $ABCD$.Gọi $M,N$ là các điểm lần lượt thuộc $AB$ và $CD$ sao cho $\overrightarrow {MA}=-2.\overrightarrow {MB},\overrightarrow {ND}=-2.\overrightarrow {NC}$.Các điểm $I,J,K$ lần lượt thuộc $AD,MN,BC$ sao cho $\overrightarrow {IA}=k.\overrightarrow {ID},\overrightarrow {JM}=k.\overrightarrow {JN},\overrightarrow {KB}=k.\overrightarrow {KC}$.Chứng minh rằng các điểm $I,J,K$ thẳng hàng.
Đề bài: Cho tứ diện $ABCD$.Gọi $M,N$ là các điểm lần lượt thuộc $AB$ và $CD$ sao cho $\overrightarrow {MA}=-2.\overrightarrow {MB},\overrightarrow {ND}=-2.\overrightarrow {NC}$.Các điểm $I,J,K$ lần lượt thuộc $AD,MN,BC$ sao cho $\overrightarrow {IA}=k.\overrightarrow {ID},\overrightarrow {JM}=k.\overrightarrow {JN},\overrightarrow {KB}=k.\overrightarrow {KC}$.Chứng minh rằng … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD$.Gọi $M,N$ là các điểm lần lượt thuộc $AB$ và $CD$ sao cho $\overrightarrow {MA}=-2.\overrightarrow {MB},\overrightarrow {ND}=-2.\overrightarrow {NC}$.Các điểm $I,J,K$ lần lượt thuộc $AD,MN,BC$ sao cho $\overrightarrow {IA}=k.\overrightarrow {ID},\overrightarrow {JM}=k.\overrightarrow {JN},\overrightarrow {KB}=k.\overrightarrow {KC}$.Chứng minh rằng các điểm $I,J,K$ thẳng hàng.
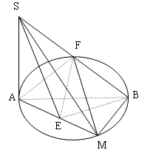
Đề bài: Cho đường tròn đường kính $AB=2R$ chứa trong mặt phẳng $(\alpha) ,SA$ vuông góc với mặt phẳng $(\alpha) ,SA=h$ với $0
Đề bài: Cho đường tròn đường kính $AB=2R$ chứa trong mặt phẳng $(\alpha) ,SA$ vuông góc với mặt phẳng $(\alpha) ,SA=h$ với $0 Lời giải Gọi $E,F$ theo thứ tự là trung điểm của $AM,SB$Nhận xét rằng dựa trên tính chất đường trung tuyến trong tam giác vuông ta có :$AF=\frac{1}{2} SB$ và $MF=\frac{1}{2} SB=\frac{\sqrt{h^2+4R^2} }{2} $$\Rightarrow MF=AF\Leftrightarrow … [Đọc thêm...] vềĐề bài: Cho đường tròn đường kính $AB=2R$ chứa trong mặt phẳng $(\alpha) ,SA$ vuông góc với mặt phẳng $(\alpha) ,SA=h$ với $0
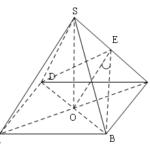
Đề bài: Trong mặt phẳng $(P)$ cho hình thoi $ABCD,AB=a,BD=\frac{2a\sqrt{3} }{3} ,O$ là giao điểm của hai đường chéo $AC,BD.$Trên đường thẳng vuông góc với $(P)$ tại $O$, ta lấy một điểm $S$ biết $SB=a$$a.$ Chứng minh tam giác $ASC$ là tam giác vuông$b.$ Chứng minh $(SBC)\bot (SDC)$
Đề bài: Trong mặt phẳng $(P)$ cho hình thoi $ABCD,AB=a,BD=\frac{2a\sqrt{3} }{3} ,O$ là giao điểm của hai đường chéo $AC,BD.$Trên đường thẳng vuông góc với $(P)$ tại $O$, ta lấy một điểm $S$ biết $SB=a$$a.$ Chứng minh tam giác $ASC$ là tam giác vuông$b.$ Chứng minh $(SBC)\bot (SDC)$ Lời giải $a.$ Ta có : $AB=SB$ và $OD$ chung nên hai tam giác vuông $AOB$ và $SOB$ … [Đọc thêm...] vềĐề bài: Trong mặt phẳng $(P)$ cho hình thoi $ABCD,AB=a,BD=\frac{2a\sqrt{3} }{3} ,O$ là giao điểm của hai đường chéo $AC,BD.$Trên đường thẳng vuông góc với $(P)$ tại $O$, ta lấy một điểm $S$ biết $SB=a$$a.$ Chứng minh tam giác $ASC$ là tam giác vuông$b.$ Chứng minh $(SBC)\bot (SDC)$