Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Hình học không gian

Đề bài: Cho hình chóp $S.ABC$ có $SA=2a$ và vuông góc với mặt phẳng $(ABC)$,đáy $ABC$ là tam giác vuông cân tại $B$ với $AB=a$.Gọi $M$ là trung điểm của $AC$$a.$ Hãy dựng đoạn vuông góc chung của $SM,BC$$b.$ Tính độ dài đoạn vuông góc chung của $SM,BC$

Ngày Thuộc chủ đề:Hình học không gian Tag với:

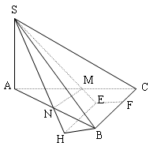
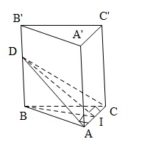
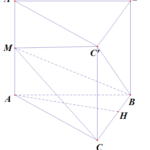
Đề bài: Cho hình chóp $S.ABC$ có $SA=2a$ và vuông góc với mặt phẳng $(ABC)$,đáy $ABC$ là tam giác vuông cân tại $B$ với $AB=a$.Gọi $M$ là trung điểm của $AC$$a.$ Hãy dựng đoạn vuông góc chung của $SM,BC$$b.$ Tính độ dài đoạn vuông góc chung của $SM,BC$ Lời giải $a.$ Để dựng đoạn vuông góc chung của $SM,BC$ ta có thể lựa chọn một trong hai cách trình bày sau:Cách … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$ có $SA=2a$ và vuông góc với mặt phẳng $(ABC)$,đáy $ABC$ là tam giác vuông cân tại $B$ với $AB=a$.Gọi $M$ là trung điểm của $AC$$a.$ Hãy dựng đoạn vuông góc chung của $SM,BC$$b.$ Tính độ dài đoạn vuông góc chung của $SM,BC$

Đề bài: Cho hình chóp tam giác $S.ABC$ đáy là tam giác vuông $ABC$ tại $A$ và $AB=3a, BC=4a$. Biết rằng mặt phẳng $(SBC)$ vuông góc với $(ABC)$. Giả sử $SB=2a\sqrt{3}$ và $\widehat{SBC}=30^0$.Tìm thể tích hình chóp $S.ABC$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

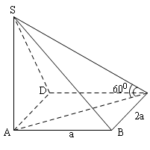
Đề bài: Cho hình chóp tam giác $S.ABC$ đáy là tam giác vuông $ABC$ tại $A$ và $AB=3a, BC=4a$. Biết rằng mặt phẳng $(SBC)$ vuông góc với $(ABC)$. Giả sử $SB=2a\sqrt{3}$ và $\widehat{SBC}=30^0$.Tìm thể tích hình chóp $S.ABC$. Lời giải Do $(SBC) \bot (ABC)$ và $(SBC) \cap (ABC)=BC$, nên nếu kẻ $SH \bot BC (H\in BC)\Rightarrow  SH\bot (ABC)$.Ta có $SH=SB. \sin … [Đọc thêm...] vềĐề bài: Cho hình chóp tam giác $S.ABC$ đáy là tam giác vuông $ABC$ tại $A$ và $AB=3a, BC=4a$. Biết rằng mặt phẳng $(SBC)$ vuông góc với $(ABC)$. Giả sử $SB=2a\sqrt{3}$ và $\widehat{SBC}=30^0$.Tìm thể tích hình chóp $S.ABC$.

Đề bài: Đáy của lăng trụ đứng $ABC.A'B'C'$ là một tam giác cân đỉnh $B$, $BA=BC=7$, $AC=2$. Qua $AC$ ta vẽ một mặt phẳng tạo với đáy dưới một góc $30^0$, cắt cạnh bên tại $D$. Tìm diện tích thiết diện và độ dài $BD$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Đáy của lăng trụ đứng $ABC.A'B'C'$ là một tam giác cân đỉnh $B$, $BA=BC=7$, $AC=2$. Qua $AC$ ta vẽ một mặt phẳng tạo với đáy dưới một góc $30^0$, cắt cạnh bên tại $D$. Tìm diện tích thiết diện và độ dài $BD$. Lời giải Ta có:Kẻ $BI$ vuông góc với $AC$ thì $I$ là trung điểm của $AC$. $BI$ là hình chiếu của $DI$ trên đáy nên $DI$ vuông góc với … [Đọc thêm...] vềĐề bài: Đáy của lăng trụ đứng $ABC.A'B'C'$ là một tam giác cân đỉnh $B$, $BA=BC=7$, $AC=2$. Qua $AC$ ta vẽ một mặt phẳng tạo với đáy dưới một góc $30^0$, cắt cạnh bên tại $D$. Tìm diện tích thiết diện và độ dài $BD$.

Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$. Gọi $M$ là trung điểm của $AA'$. Chứng minh rằng thiết diện $C'MB$ chia lăng trụ thành hai phần tương đương.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$. Gọi $M$ là trung điểm của $AA'$. Chứng minh rằng thiết diện $C'MB$ chia lăng trụ thành hai phần tương đương. Lời giải Trong (ABC) dựng AH $\bot$ BC$V_{M.ABC}=\frac13MA.S_{ABC}=\frac16V_{ABC.A'B'C'}$$V_{M.CBC'}=\frac13d(M,(CBC')).S_{CBC'}= \frac13AH.S_{CBC'} = \frac13V_{ABC.A'B'C'} $$\Rightarrow … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$. Gọi $M$ là trung điểm của $AA'$. Chứng minh rằng thiết diện $C'MB$ chia lăng trụ thành hai phần tương đương.

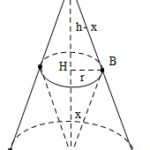
Đề bài: Cho hình nón đỉnh $S$ đáy là hình tròn $(O;R)$. Một mặt phẳng $(\alpha)$ vuông góc với $SO$ tại điểm $H$ thuộc đoạn $SO$ và cất hình nón theo đường tròn $(C)$. Đặt $OH=x (0

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình nón đỉnh $S$ đáy là hình tròn $(O;R)$. Một mặt phẳng $(\alpha)$ vuông góc với $SO$ tại điểm $H$ thuộc đoạn $SO$ và cất hình nón theo đường tròn $(C)$. Đặt $OH=x (0 Lời giải Gọi $r$ là bán kính đáy của $(C), V$ là thể tích hình nón đỉnh $O$ đáy là hình tròn $(C)$, ta có: $\frac{r}{R}=\frac{SH}{SO}=\frac{h-x}{h} \Rightarrow r=\frac{(h-x)R}{h}$   … [Đọc thêm...] vềĐề bài: Cho hình nón đỉnh $S$ đáy là hình tròn $(O;R)$. Một mặt phẳng $(\alpha)$ vuông góc với $SO$ tại điểm $H$ thuộc đoạn $SO$ và cất hình nón theo đường tròn $(C)$. Đặt $OH=x (0

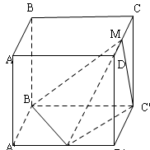
Đề bài: Cho lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $M$ là trung điểm $CD$ và $N$ là trung điểm $A'D'$. Hãy tính góc giữa hai đường thẳng $B'M$ và $C'N$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $M$ là trung điểm $CD$ và $N$ là trung điểm $A'D'$. Hãy tính góc giữa hai đường thẳng $B'M$ và $C'N$. Lời giải  Đặt $\overrightarrow{A'B'}=\overrightarrow{i}; \overrightarrow{A'D'}=\overrightarrow{j }; \overrightarrow{A'A}=\overrightarrow{k}$, ta … [Đọc thêm...] vềĐề bài: Cho lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $M$ là trung điểm $CD$ và $N$ là trung điểm $A'D'$. Hãy tính góc giữa hai đường thẳng $B'M$ và $C'N$.

Đề bài: Hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, các kích thước $AB=1,BC=2a$.Hai mặt bên $SAB,SAD$ vuông góc với đáy còn cạnh bên $SC$ tạo với đáy một góc $60^0$$a.$ Tính đường cao  hình chóp$b.$ Tính góc giữa hai mặt bên $(SBC),(SCD)$ hợp với mặt phẳng đáy

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, các kích thước $AB=1,BC=2a$.Hai mặt bên $SAB,SAD$ vuông góc với đáy còn cạnh bên $SC$ tạo với đáy một góc $60^0$$a.$ Tính đường cao  hình chóp$b.$ Tính góc giữa hai mặt bên $(SBC),(SCD)$ hợp với mặt phẳng đáy Lời giải $a.$ Dễ thấy :$\left.\begin{matrix}(SAB)\bot (ABCD) \\ (SAD)\bot (ABCD)\end{matrix}\right\} … [Đọc thêm...] vềĐề bài: Hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, các kích thước $AB=1,BC=2a$.Hai mặt bên $SAB,SAD$ vuông góc với đáy còn cạnh bên $SC$ tạo với đáy một góc $60^0$$a.$ Tính đường cao  hình chóp$b.$ Tính góc giữa hai mặt bên $(SBC),(SCD)$ hợp với mặt phẳng đáy

Đề bài: Cho tứ giác $ABCD$ nằm trong mặt phẳng $(P)$ và một điểm $S$ nằm ngoài mặt phẳng $(P).$Nối $(S)$ với các đỉnh của tứ giác; trên hình vẽ có tất cả bao nhiêu mặt phẳng

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho tứ giác $ABCD$ nằm trong mặt phẳng $(P)$ và một điểm $S$ nằm ngoài mặt phẳng $(P).$Nối $(S)$ với các đỉnh của tứ giác; trên hình vẽ có tất cả bao nhiêu mặt phẳng Lời giải ĐS : có $7$ mặt phẳngCần giải chi tiết … [Đọc thêm...] vềĐề bài: Cho tứ giác $ABCD$ nằm trong mặt phẳng $(P)$ và một điểm $S$ nằm ngoài mặt phẳng $(P).$Nối $(S)$ với các đỉnh của tứ giác; trên hình vẽ có tất cả bao nhiêu mặt phẳng

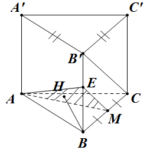
Đề bài: Cho lăng trụ đứng $ABC.A'B'C'$ đáy là tam giác vuông có $BA=BC=a$; cạnh bên $AA'=a\sqrt{2}$. Gọi $M$ là trung điểm của $BC$. Tính khoảng cách giữa hai đường thẳng $AM, BC'$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho lăng trụ đứng $ABC.A'B'C'$ đáy là tam giác vuông có $BA=BC=a$; cạnh bên $AA'=a\sqrt{2}$. Gọi $M$ là trung điểm của $BC$. Tính khoảng cách giữa hai đường thẳng $AM, BC'$. Lời giải Gọi $E'$ là trung điểm của $BB'$.Ta có : $EM //B'C\Rightarrow B'C // (AEM)$$\Rightarrow d(B'C, AM)=d(B'C,(AEM))=d(C,(AEM))=d(B,(AEM))$ (Vì $MB=MC$)Do … [Đọc thêm...] vềĐề bài: Cho lăng trụ đứng $ABC.A'B'C'$ đáy là tam giác vuông có $BA=BC=a$; cạnh bên $AA'=a\sqrt{2}$. Gọi $M$ là trung điểm của $BC$. Tính khoảng cách giữa hai đường thẳng $AM, BC'$.