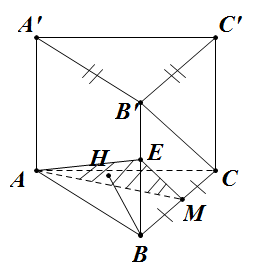
Đề bài: Cho lăng trụ đứng $ABC.A'B'C'$ đáy là tam giác vuông có $BA=BC=a$; cạnh bên $AA'=a\sqrt{2}$. Gọi $M$ là trung điểm của $BC$. Tính khoảng cách giữa hai đường thẳng $AM, BC'$.

Lời giải

Gọi $E’$ là trung điểm của $BB’$.
Ta có : $EM //B’C\Rightarrow B’C // (AEM)$
$\Rightarrow d(B’C, AM)=d(B’C,(AEM))=d(C,(AEM))=d(B,(AEM))$ (Vì $MB=MC$)
Do $ABC $ là tam giác vuông tại $B$, nên tứ diện $BAEM$ có $BA,BE,BM$ đôi một vuông góc với nhau.

Gọi $BH $ là chiều cao kẻ từ $B$ của tứ diện trên $(H \in (AEM))$ thì dễ dàng nhận thấy:
$\frac{1}{BH^2}=\frac{1}{BA^2}+\frac{1}{BE^2}+\frac{1}{BM^2}=\frac{1}{a^2}+\frac{1}{\frac{a^2}{2}}+\frac{1}{\frac{a^2}{4}}=\frac{7}{a^2}$
$ \Rightarrow  BH=\frac{a\sqrt{7}}{7}\Rightarrow d(AM,B’C)=\frac{a\sqrt{7}}{7}$