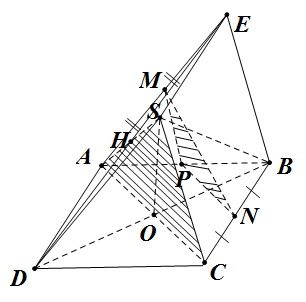
Đề bài: Cho hình chóp tứ giác đều $S.ABCD$, cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ tương ứng là trung điểm của $AE, BC$. Tìm khoảng cách theo $a$ giữa hai đường thẳng $MN,AC$.

Lời giải

Goi $P$ là trung điểm của $AB$ khi đó $MP//EB  (1)$
Ta có: $SE// DA; SE=DA\Rightarrow SE//BC; SE=BC$
$\Rightarrow SEBC $là hình binh hành $\Rightarrow EB //SC  (2)$
Vậy từ $(1),(2)$ suy ra $MP//SC$.
Lại có $PN//AC\Rightarrow (MPN)//(SAC)  (3)$
Từ $(3)$ suy ra $d(MN,AC)=d((MNP),(SAC))=d(H,(SAC))  (4)$
Ở đây $H$ là giao điểm của $BD, PN$.

Vì $HO\bot (SAC)\Rightarrow d(H,(SAC))=HO= \frac{1}{4}BD=\frac{a\sqrt{2}}{4}$,
ở đây $O$ là giao điểm $AC,BD$. Từ  $(4)$ suy ra: $d(MN,AC)=\frac{a\sqrt{2}}{4}$.