Đề bài: Trong không gian cho hai tia $Ax,By$ chéo nhau và vuông góc với nhau,$AB$ là đoạn vuôn góc chung.Trên $Ax,By$ theo thứ tự, ta lấy các điểm $M,P$ thỏa mãn hệ thức $2AM.AP=AB^2$Chứng minh rằng khoảng cách giữa trung điểm $O$ của đoạn thẳng $AB$ đến đường thẳng $MP$ thì bằng $\frac{1}{2} AB$

Lời giải

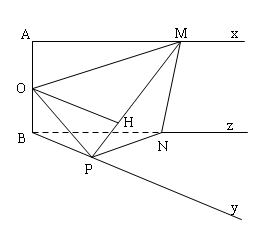
Kẻ tia $Bz//Ax$ và lấy trên $Bz$ điểm $N$ sao cho $BN=AM$
$AB\bot (By,Bz)\Rightarrow  AB\bot NP$
$MN//AB$
$\Rightarrow  MN\bot NP\Rightarrow  \widehat{MNP}=90^0 $
Mặt khác ta cũng có $Bz\bot By$
$\Rightarrow  \widehat{PBN}=90^0 $
Đặt $MP=a,OP=b,MO=c,AB=MN=2h$
$AM=BN=v, BP=u$
Ta có :
$b^2=h^2+u^2; c^2=h^2+v^2$
$a^2=4h^2+PN^2=4h^2+u^2+v^2$
Từ các hệ thức này, kết hợp với giả thiết $2u.v=4h^2$ và kết quả của việc áp dụng định lí cosin vào tam giác $OMP :$
$a^2=b^2+c^2-2bc.cos\widehat{POM} $ ta được :
$cos\widehat{POM}=\frac{b^2+c^2-a^2}{2bc}  $
Ta tính diện tích $\Delta POM$
$S_{POM}=\frac{1}{2} bcsin\widehat{POM} =\frac{1}{2} bc\sqrt{1-\frac{(b^2+c^2-a^2)^2}{4b^2c^2} } $
$S_{PM}=\frac{1}{4} \sqrt{4b^2c^2-(b^2+c^2-a^2)^2} $
$S_{POM}=\frac{1}{4} \sqrt{4(h^2+u^2)(h^2+v^2)-4h^2} $
$S_{POM}=\frac{1}{4} \sqrt{4h^2u^2+4h^2v^2+16h^2} =\frac{ah}{2}        (1)$
Mặt khác $S_{POM}=\frac{1}{2} (OH.a)$ vì $OH\bot MP       (2)$
Từ $(1),(2)$ suy ra : $OH=h\Rightarrow  OH=\frac{AB}{2} $