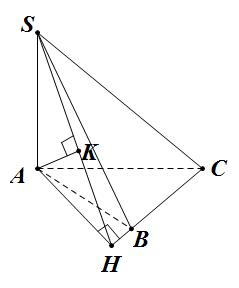
Đề bài: Cho hình chóp $S.ABC$ có $SA=3a$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Giả sử $AB=BC=2a; \widehat{ABC}=120^0$ tìm khoảng cách từ $A$ đến mặt phẳng $(SBC)$.

Lời giải

Kẻ $AH \bot BC \Rightarrow SH \bot BC$ (định lí ba đường vuông góc).
Lại có: $BC \bot (SAH)\Rightarrow (SBC)\bot (SAH)$.
Do $(SBC) \cap (SAH)=AH,$
nên nếu kẻ $AK \bot SH( K \in SH) \Rightarrow AK \bot (SBC)$.

Vậy $d(A, (SBC))=AK$.
Ta có : $AH =AB \sin 60^0=2a\frac{\sqrt{3}}{2}=a\sqrt{3}$.
Theo hệ thức lượng trong tam giác vuông $SAH$ ta có:
$\frac{1}{AK^2}=\frac{1}{SA^2}+\frac{1}{SH^2}=\frac{1}{9a^2}+\frac{1}{3a^2}=\frac{4}{9a^2}\Rightarrow AK=\frac{3a}{2}$ . Do vậy $ d(A, (SBC))=\frac{3a}{2}$.