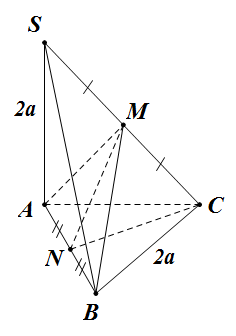
Đề bài: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B, AB=a, BC=2a$, cạnh $SA$ vuông góc với đáy và $SA=2a$. Xác định và tính độ dài đường vuông góc chung của hai đường thẳng $AB,SC$.

Lời giải
Gọi $M,N$ lần lượt là trung điểm của $SC,AB$.
ta có: $MA=MB=\frac{SC}{2}\Rightarrow MN \bot AB$.

Dễ thấy tam giác vuông $SAN$ bằng tam giác vuông $NBC\Rightarrow NS=NC\Rightarrow NM \bot SC$.
Vậy $MN$ là đường vuông góc chung của $AB,SC$. Ta có:
$SC^2=SA^2+AC^2=SA^2+AB^2+BC^2=4a^2+a^2+4a^2$
$\Rightarrow SC=3a \Rightarrow MA=\frac{3a}{2}$
Do đó: $MN^2=MA^2-AN^2=\frac{9a^2}{4}-\frac{a^2}{4}=2a^2\Rightarrow MN= a\sqrt{2}$.
