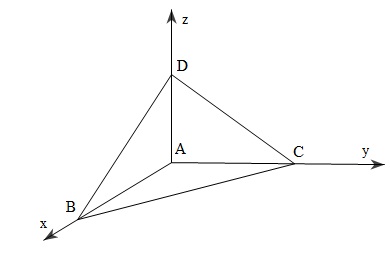
Đề bài: Cho tứ diện $ABCD$ có $AD\bot mp(ABC), AC=AD=4cm, AB=3cm, BC=5cm$. Tính khoảng cách từ $A$ đến $mp(BCD)$

Lời giải

$\Delta ABC$ vuông tại $A$ vì $BC^2=25=AB^2+AC^2$
Gắn hệ trục tọa độ như hình vẽ thì $A(0;0;0),, B(3;0;0), C(0;4;0), D(0;0;4)$
Phương trình mặt chắn $(BCD):\frac{x}{3}+\frac{y}{4}+\frac{z}{4}=1\Leftrightarrow  4x+3y+3z-12=0  $
Vậy: $d(A,mp(BCD))=\frac{|0-12|}{\sqrt{16+9+9} }=\frac{12}{\sqrt{34} }  $