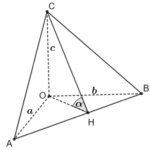
Cho tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc với nhau. Kí hiệu \(S,{S_1},{S_2},{S_3}\) lần lượt là diện tích các tam giác \(ABC,OAB,OBC,OCA\). Chứng minh rằng \(\frac{{S_1^2}}{{2S_1^2 + {S^2}}} + \frac{{S_2^2}}{{2S_2^2 + {S^2}}} + \frac{{S_3^2}}{{2S_3^2 + {S^2}}} \le \frac{3}{5}\). Lời giải Đặt \(OA = a,OB = b,OC = c\). Gọi \(H\) là hình chiếu của \(O\) … [Đọc thêm...] vềCho tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc với nhau. Kí hiệu \(S,{S_1},{S_2},{S_3}\) lần lượt là diện tích các tam giác \(ABC,OAB,OBC,OCA\).
Hình học không gian
Cho hình chóp \(S.ABC\) có \(SA \bot (ABC)\), tam giác \(ABC\) vuông tại \(B\), góc tạo bởi hai mặt phẳng \((SAC)\) và \((SBC)\) bằng \(\widehat {BAC}\). Tính \(P = \tan \widehat {BAC} \cdot \cos \widehat {ASB}\).
Cho hình chóp \(S.ABC\) có \(SA \bot (ABC)\), tam giác \(ABC\) vuông tại \(B\), góc tạo bởi hai mặt phẳng \((SAC)\) và \((SBC)\) bằng \(\widehat {BAC}\). Tính \(P = \tan \widehat {BAC} \cdot \cos \widehat {ASB}\). Lời giải Gọi \(H,K\) lần lượt là hình chiếu của \(A\) xuống \(SB,SC\). Từ đây dẫn đến \(SC \bot \left( {AHK} \right)\) hay \(HK \bot SC\), vì thế … [Đọc thêm...] vềCho hình chóp \(S.ABC\) có \(SA \bot (ABC)\), tam giác \(ABC\) vuông tại \(B\), góc tạo bởi hai mặt phẳng \((SAC)\) và \((SBC)\) bằng \(\widehat {BAC}\). Tính \(P = \tan \widehat {BAC} \cdot \cos \widehat {ASB}\).
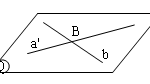
Đề bài: Giả sử $a$ và $b$ là hai đường chéo nhau. Chứng minh rằng tồn tại duy nhất một mặt phẳng $(P)$ chứa $a$ và một mặt phẳng $(Q)$ chứa $b$ sao cho $(P)//(Q)$
Đề bài: Giả sử $a$ và $b$ là hai đường chéo nhau. Chứng minh rằng tồn tại duy nhất một mặt phẳng $(P)$ chứa $a$ và một mặt phẳng $(Q)$ chứa $b$ sao cho $(P)//(Q)$ Lời giải Qua một điểm $A\in a$, vẽ đường thẳng $b'$ song song với $b$ và qua một điểm $B\in b$ vẽ đường thẳng $a'$ song song với $a$. Gọi $(P)$= mp$(a,b')$, $(Q)$= mp$(b,a')$ thì rõ ràng $(P)\parallel … [Đọc thêm...] vềĐề bài: Giả sử $a$ và $b$ là hai đường chéo nhau. Chứng minh rằng tồn tại duy nhất một mặt phẳng $(P)$ chứa $a$ và một mặt phẳng $(Q)$ chứa $b$ sao cho $(P)//(Q)$
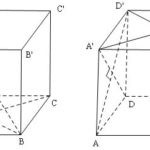
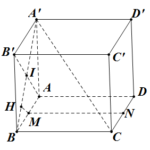
Đề bài: Cho hình lập phương $ABCD.A’B’C’D’$ với cạnh bằng $a$.$1.$ Hãy tính khoảng cách giữa hai đường thẳng $AA’$ và $BD’$$2.$ Chứng minh rằng đường chéo $BD’$ vuông góc với mặt phẳng $(DA’C’).$
Đề bài: Cho hình lập phương $ABCD.A’B’C’D’$ với cạnh bằng $a$.$1.$ Hãy tính khoảng cách giữa hai đường thẳng $AA’$ và $BD’$$2.$ Chứng minh rằng đường chéo $BD’$ vuông góc với mặt phẳng $(DA’C’).$ Lời giải $1.$ Gọi $I, J$ lần lượt là trung điểm của $AA’, BD’$. Dễ thấy $IJ$ là chân đường vuông góc chung của $AA’$ và $BD’$. Vậy khoảng cách cần tính chính là đoạn $IJ$. … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A’B’C’D’$ với cạnh bằng $a$.$1.$ Hãy tính khoảng cách giữa hai đường thẳng $AA’$ và $BD’$$2.$ Chứng minh rằng đường chéo $BD’$ vuông góc với mặt phẳng $(DA’C’).$
Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tìm khoảng cách giữa hai đường thẳng $A'C, MN$.
Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tìm khoảng cách giữa hai đường thẳng $A'C, MN$. Lời giải Ta có $BC//MN\Rightarrow MN//(A'BC) \Rightarrow d(MN,A'C)=d(M,(A'BC))=d(M,(A'BC)) (1)$Ta có: $AI \bot A'B (A'B \cap AB'=I)$.Ta lại có: $ BC \bot (BAA'B) \Rightarrow BC \bot … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tìm khoảng cách giữa hai đường thẳng $A'C, MN$.
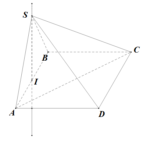
Đề bài: Trong mặt phẳng $(P)$ cho hình vuông $ABCD$ cạnh bằng $a$. Qua trung điểm $I$ của cạnh $AB$ dựng đường thẳng $d$ vuông góc với mặt phẳng $(ABCD)$. Trên $d$ lấy điểm $S$ sao cho $SI=\frac{a\sqrt{3}}{2}$.1) Tìm thể tích hình chóp $S.ACD$.2) Tìm khoảng cách từ $C$ đến $(SAD)$.
Đề bài: Trong mặt phẳng $(P)$ cho hình vuông $ABCD$ cạnh bằng $a$. Qua trung điểm $I$ của cạnh $AB$ dựng đường thẳng $d$ vuông góc với mặt phẳng $(ABCD)$. Trên $d$ lấy điểm $S$ sao cho $SI=\frac{a\sqrt{3}}{2}$.1) Tìm thể tích hình chóp $S.ACD$.2) Tìm khoảng cách từ $C$ đến $(SAD)$. Lời giải 1) … [Đọc thêm...] vềĐề bài: Trong mặt phẳng $(P)$ cho hình vuông $ABCD$ cạnh bằng $a$. Qua trung điểm $I$ của cạnh $AB$ dựng đường thẳng $d$ vuông góc với mặt phẳng $(ABCD)$. Trên $d$ lấy điểm $S$ sao cho $SI=\frac{a\sqrt{3}}{2}$.1) Tìm thể tích hình chóp $S.ACD$.2) Tìm khoảng cách từ $C$ đến $(SAD)$.
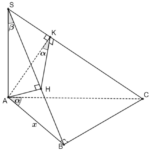
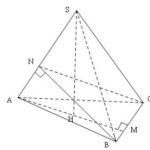
Đề bài: Cho hình chóp đều $S.ABC$ đỉnh $S$ có các cạnh đáy đều bằng $a$, đường cao hình chóp $SH = h.$$a$) Xác định thiết diện tạo bởi hình chóp với mặt phẳng ($P$) qua cạnh đáy $BC$ và vuông góc với cạnh bên $SA.$$b)$ Nếu tỉ số $\frac{h}{a} = \sqrt 3 $ thì mặt phẳng ($P$) chia thể tích hình chóp theo tỉ số nào?
Đề bài: Cho hình chóp đều $S.ABC$ đỉnh $S$ có các cạnh đáy đều bằng $a$, đường cao hình chóp $SH = h.$$a$) Xác định thiết diện tạo bởi hình chóp với mặt phẳng ($P$) qua cạnh đáy $BC$ và vuông góc với cạnh bên $SA.$$b)$ Nếu tỉ số $\frac{h}{a} = \sqrt 3 $ thì mặt phẳng ($P$) chia thể tích hình chóp theo tỉ số nào? Lời giải $a$. Vì $SABC$ là hình chóp đều nên chân … [Đọc thêm...] vềĐề bài: Cho hình chóp đều $S.ABC$ đỉnh $S$ có các cạnh đáy đều bằng $a$, đường cao hình chóp $SH = h.$$a$) Xác định thiết diện tạo bởi hình chóp với mặt phẳng ($P$) qua cạnh đáy $BC$ và vuông góc với cạnh bên $SA.$$b)$ Nếu tỉ số $\frac{h}{a} = \sqrt 3 $ thì mặt phẳng ($P$) chia thể tích hình chóp theo tỉ số nào?
Đề bài: Cho tứ diện $OABC$ có $OA, OB, OC$ vuông góc nhau từng đôi một, với $OA=a, OB=b$. Gọi $M$ là trung điểm $BC$. Xác định và tính đoạn vuông góc của $OC$ và $AM$.
Đề bài: Cho tứ diện $OABC$ có $OA, OB, OC$ vuông góc nhau từng đôi một, với $OA=a, OB=b$. Gọi $M$ là trung điểm $BC$. Xác định và tính đoạn vuông góc của $OC$ và $AM$. Lời giải vẽ $MM' \parallel OC (M'\in OB)$, ta có: $OC \parallel (AM'M).$Vẽ $OH\bot AM'$, suy ra $OH\bot (AMM')$.Vẽ $HI \parallel OC(I\in AM)$ và $IJ \parallel OH(J\in OC)$, ta có $IJ$ là đoạn vuông … [Đọc thêm...] vềĐề bài: Cho tứ diện $OABC$ có $OA, OB, OC$ vuông góc nhau từng đôi một, với $OA=a, OB=b$. Gọi $M$ là trung điểm $BC$. Xác định và tính đoạn vuông góc của $OC$ và $AM$.
Đề bài: Cho hai tam giác $ABC,A'B'C'$ nằm trong hai mặt phẳng phân biệt.Chứng minh rằng các đường thẳng đi qua các trung điểm của các cặp cạnh $AB'$ và $A'B,BC'$ và $B'C,CA'$ và $C'A$ song song với một mặt phẳng
Đề bài: Cho hai tam giác $ABC,A'B'C'$ nằm trong hai mặt phẳng phân biệt.Chứng minh rằng các đường thẳng đi qua các trung điểm của các cặp cạnh $AB'$ và $A'B,BC'$ và $B'C,CA'$ và $C'A$ song song với một mặt phẳng Lời giải Đặt $\overrightarrow {a},\overrightarrow {b},\overrightarrow {c} $ là các véctơ chỉ phương của các … [Đọc thêm...] vềĐề bài: Cho hai tam giác $ABC,A'B'C'$ nằm trong hai mặt phẳng phân biệt.Chứng minh rằng các đường thẳng đi qua các trung điểm của các cặp cạnh $AB'$ và $A'B,BC'$ và $B'C,CA'$ và $C'A$ song song với một mặt phẳng
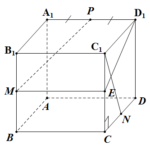
Đề bài: Cho hình lập phương $ABCD. A_1B_1C_1D_1$. Gọi $M,N,P$ lần lượt là trung điểm của $BB_1, CD, A_1D_1$. Chứng minh $MP \bot C_1N$.
Đề bài: Cho hình lập phương $ABCD. A_1B_1C_1D_1$. Gọi $M,N,P$ lần lượt là trung điểm của $BB_1, CD, A_1D_1$. Chứng minh $MP \bot C_1N$. Lời giải Gọi $E$ là trung điểm của $CC_1$.ta có: $ME// BC\Rightarrow ME// A_1D_1$.Gọi $(Q)$ là mặt phẳng $MED_1A_1\Rightarrow MP \in (Q) (1)$Dễ thấy hai tam giác vuông $C_1CN; D_1C_1E$ bằng nhau $\Rightarrow … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD. A_1B_1C_1D_1$. Gọi $M,N,P$ lần lượt là trung điểm của $BB_1, CD, A_1D_1$. Chứng minh $MP \bot C_1N$.