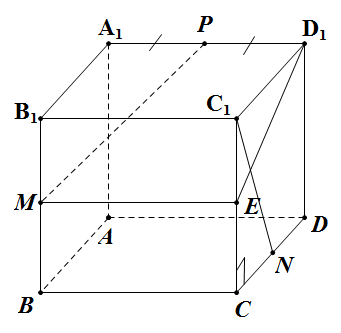
Đề bài: Cho hình lập phương $ABCD. A_1B_1C_1D_1$. Gọi $M,N,P$ lần lượt là trung điểm của $BB_1, CD, A_1D_1$. Chứng minh $MP \bot C_1N$.

Lời giải

Gọi $E$ là trung điểm của $CC_1$.
ta có: $ME// BC\Rightarrow ME// A_1D_1$.
Gọi $(Q)$ là mặt phẳng $MED_1A_1\Rightarrow MP \in (Q)  (1)$

Dễ thấy hai tam giác vuông $C_1CN; D_1C_1E$ bằng nhau
$\Rightarrow \widehat{CNC_1}=\widehat{C_1ED_1}=\widehat{CC_1N}+\widehat{C_1NC}=90^0\Rightarrow C_1N \bot ED_1  (2)$
Do $ME// BC \Rightarrow ME \bot (CDD_1C_1) \Rightarrow ME \bot C_1N   (3)$
Từ $(2),(3)$ suy ra : $C_1N \bot (Q)\Rightarrow C_1N \bot MP$