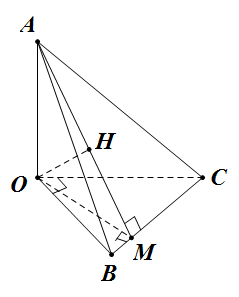
Đề bài: Cho tứ diện $OABC$ trong đó $OA, OB, OC$ đôi một vuông góc với nhau. Kẻ $OH \bot (ABC)$.1. Chứng minh $H$ là trực tâm tam giác $ABC$.2. Chứng minh hệ thức  $\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}+\frac{1}{OC^2}$.

Lời giải

1.Kẻ $OH \bot (ABC), AH \cap BC=M$.

Ta có : $OH \bot BC; BC \bot OA$ Vì $( OA \bot ABC)$.
(Suy từ $OA \bot OB, OA \bot OC$)
$\Rightarrow BC \bot (AOH) \Rightarrow BC \bot AH$
lập luận tương tự ta có $BH \bot AC$.
Vậy $H$ là trực tâm của tam giác $ABC\Rightarrow $ đpcm.
2. Theo định lí ba đường vuông góc, suy ra $MO \bot BC$
Theo hệ thức lượng trong tam giác vuông $AOM$ ta có:
  $\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OM^2}  (1)$
Lại theo hệ thức lượng trong tam giác vuông $OAB$ ta có:
  $\frac{1}{OM^2}=\frac{1}{OB^2}+\frac{1}{OC^2}  (2)$
Từ $(1),(2)$ suy ra $\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}+\frac{1}{OC^2}\Rightarrow $đpcm.