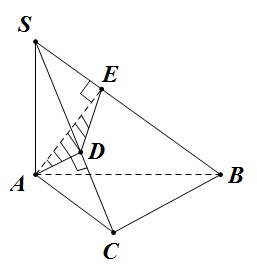
Đề bài: Cho hình chóp $S.ABC$, trong đó đáy $ABC$ là tam giác vuông tại $C$, hai mặt bên $(SAC),(SAB)$ cùng vuông góc với đáy $ABC$. Gọi $D,E$ lần lượt là hình chiếu của $A$ trên $SC,SB$. Chứng minh $(SAB) \bot (ADE)$

Lời giải

Vì $(SAB) \bot (ABC); (SAC) \bot (ABC)$,
mà $(SAB) \cap (SAC)=SA$, nên $SA \bot (ABC)$.
Vì $BC \bot CA \Rightarrow BC \bot (SAC)$.
$\Rightarrow (SBC) \bot (SAC)$. Do $AD \bot SC$, mà $SC=(SAC)\cap (SBC)\Rightarrow AD \bot (SBC)$
$\Rightarrow AD \bot SB (1)$
Từ $(1)$ kết hợp với $AE \bot SB$ suy ra:
$SB \bot (ADE)\Rightarrow (SAB) \bot (ADE) \Rightarrow $ đpcm.
