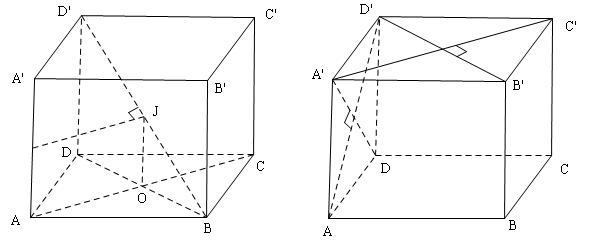
Đề bài: Cho hình lập phương $ABCD.A’B’C’D’$ với cạnh bằng $a$.$1.$ Hãy tính khoảng cách giữa hai đường thẳng $AA’$ và $BD’$$2.$ Chứng minh rằng đường chéo $BD’$ vuông góc với mặt phẳng $(DA’C’).$

Lời giải

$1.$ Gọi $I, J$ lần lượt là trung điểm của $AA’, BD’$. Dễ thấy $IJ$ là chân đường vuông góc chung của $AA’$ và $BD’$. Vậy khoảng cách cần tính chính là đoạn $IJ$. Ta có: $IJ = OA = \frac{{a\sqrt 2 }}{2}$
$2.$ Có $A’C’ \bot B’D’ \Rightarrow A’C’ \bot BD’\,\,(1)$
Có: $\left\{ \begin{array}{l}
DA’ \bot AD’\\
DA’ \bot AB
\end{array} \right. \Rightarrow DA’ \bot (D’AB) \Rightarrow DA’ \bot BD’\,(2)$
Từ ($1$) và ($2$) $ \Rightarrow BD’ \bot (DA’C’)$