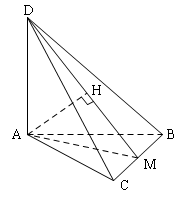
Đề bài: Trong mặt phẳng $(P)$ cho tam giác cân $ABC$, đỉnh $A$.Trên đường vuông góc với $(P)$ kẻ từ $A$, có một điểm $D$.Gọi $M$ là trung điểm của $BC,H$ là hình chiếu của $A$ trên $DM$$a.$ Chứng minh $BC\bot (ADM)$$b.$ Chứng minh $AH\bot (BCD)$

Lời giải

$a.$ Dễ thấy hai tam giác vuông $DAB,DAC$ bằng nhau, cho ta $BD=DC$, suy ra tam giác $DBC$ cân đỉnh $B$.Vì $M$ là trung điểm của $BC$ nên ta có $DM\bot BC        (1)$
Theo giả thiết, ta giác $ABC$ cân, đỉnh $A$ cho ta $AM\bot BC      (2)$
Từ $(1),(2)$ ta có $BC\bot (ADM)$
$b) $
$\left.\begin{matrix} BC\bot (ADM)\\ AH\subset  (ADM)\end{matrix}\right\}\Rightarrow  AH\bot BC       (3)$
Giả thiết cho ta $AH\bot DM      (4)$
Từ $(3),(4)$ suy ra $AH\bot (BCD)$