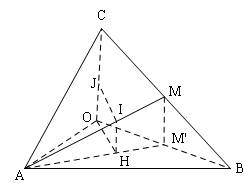
Đề bài: Cho tứ diện $OABC$ có $OA, OB, OC$ vuông góc nhau từng đôi một, với $OA=a, OB=b$. Gọi $M$ là trung điểm $BC$. Xác định và tính đoạn vuông góc của $OC$ và $AM$.

Lời giải

vẽ $MM’ \parallel OC (M’\in OB)$, ta có: $OC \parallel (AM’M).$
Vẽ $OH\bot AM’$, suy ra $OH\bot (AMM’)$.
Vẽ $HI \parallel OC(I\in AM)$ và $IJ \parallel OH(J\in OC)$, ta có $IJ$ là đoạn vuông góc chung của $OC$ và $AM$. Thật vậy, $IJ \parallel OH$ nên $IJ\bot OC$ và $IJ\bot (AM’M)$, do đó $IJ\bot AM$.
Tam giác $OAM’$ vuông có $OH$ là đường cao nên:
$\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OM’^2}=\frac{1}{a^2}+\frac{4}{b^2},$ suy ra $IJ=OH=\frac{ab}{\sqrt{4a^2+b^2} }.$