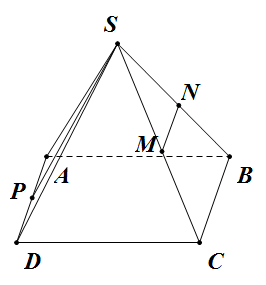
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a; SA$ vuông góc với đáy. Gọi $M,N$ là trung điểm của $AD, SC$. Chứng minh mặt phẳng $(SAC)$ vuông góc với mặt phẳng $(SMB)$.

Lời giải

Giả sử $AC\cap MB=I$.
Vì $MA=MD$ và do $AD//BC$,
nên theo định lí Talet suy ra $AI=\frac{1}{2}IC$
Do $AC^2=AD^2+DC^2=(a\sqrt{2})^2+a^2=3a^2$
$\Rightarrow AI^2=\frac{1}{9}AC^2=\frac{a^2}{3}$.
Ta cũng có: $MI=\frac{1}{3}MB\Rightarrow MI^2=\frac{1}{9}MB^2=\frac{1}{9}((\frac{a\sqrt{2}}{2})^2+a^2)=\frac{a^2}{6}$.
Từ đó suy ra $AI^2+MI^2=\frac{a^2}{3}+\frac{a^2}{6}=(\frac{a\sqrt{2}}{2})^2=AM^2$
Vậy $AIM$ là tam giác vuông tại $I\Rightarrow MB \bot AC  (1)$
Mặt khác $SA \bot (ABCD)\Rightarrow SA \bot MB (2)$
Từ $(1),(2)$ suy ra $MB \bot (SAC)\Rightarrow (SMB) \bot (SAC)\Rightarrow $ đpcm.