Đề bài: Giả sử $a$ và $b$ là hai đường chéo nhau. Chứng minh rằng tồn tại duy nhất một mặt phẳng $(P)$ chứa $a$ và một mặt phẳng $(Q)$ chứa $b$ sao cho $(P)//(Q)$

Lời giải

 
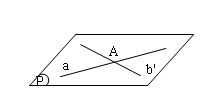
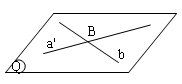
 Qua một điểm $A\in a$, vẽ đường thẳng $b’$ song song với $b$ và qua một điểm $B\in b$ vẽ đường thẳng $a’$ song song với $a$. Gọi $(P)$= mp$(a,b’)$, $(Q)$= mp$(b,a’)$ thì rõ ràng $(P)\parallel (Q)$. Giả sử còn có mp$(P’)$ và mp $(Q’)$ lần lượt qua $a$ và $b$ và song song với nhau. Khi đó ta có $b\parallel (P’)$, suy ra mp$(b,b’)$ cắt mp$(P’)$ theo giao tuyến $b”$ qua $A$ và $b”\parallel b$ (vì qua $A$ chỉ có duy nhất một đường thẳng song song với $b$). Từ đó ta có $b’$ nằm trên mp$(P’)$; mặt khác $a$ thuộc $(P’)$, vậy mp$(P’)$ trùng với mp$(P)$. Lí luận tương tự mp$(Q’)$ trùng với  mp$(Q)$.