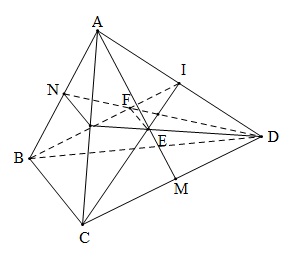
Đề bài: Cho tứ diện $ABCD$. $AM, DN$ theo thứ tự là các đường trung tuyến của các tam giác $ACD$ và $ABD$. $E\in AM, F\in DN$ sao cho $EF//BC$. Tìm tỉ số $\frac{EF}{BC}$.

Lời giải

Ta có:
Vì $EF//BC$ nên mp $BCEF$ cắt $AD$ tại $I$. Kẻ $NK//BC$ thì $K$ là trung điểm của $AC$. Vì $NK$ và $EF$ cùng song song $BC$ nên $EF//NK$. Mp $BCI$ và mp $DNK$ có chung nhau điểm $F$ nên cắt nhau theo giao tuyến $FE$, vì $FE$ và $KN$ cùng thuộc mp $\rightarrow K, E, D$  thẳng hàng. Vậy $E$ là trọng tâm $\Delta ACD$, $F$ là trọng tâm $\Delta ABD$. Suy ra: $\frac{EF}{BC}=\frac{IE}{IC}=\frac{1}{3}$.