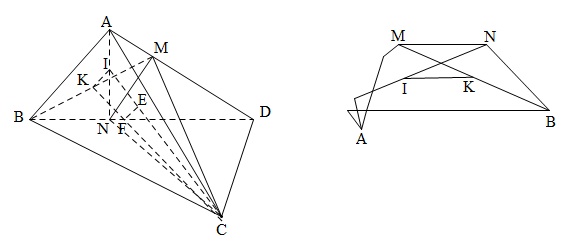
Đề bài: Trên các cạnh $AD$ và $BD$ của tứ diện $ABCD$ lấy các điểm $M, N$ sao cho $\frac{AM}{AD}=\frac{BN}{BD}=m$. Tìm khoảng cách giữa các trọng tâm tam giác $\Delta ACN$ và $\Delta BMC$ theo $AB=a$.

Lời giải
Từ giả thiết cho: $\frac{DM}{AD}=\frac{DN}{DB}=\frac{MN}{AB}\Leftrightarrow \frac{DA-AM}{DA}=\frac{MN}{a}$
$\Leftrightarrow 1-\frac{AM}{DA}=\frac{MN}{a}\Rightarrow MN=a(1-m)$
Dễ thấy $IK=\frac{1}{2}(AB-MN)=\frac{1}{2}[a-a(1-m)]=\frac{1}{2}ma$.
Gọi $E, F$ theo thứ tự là trọng tâm $\Delta ANC$ và $\Delta BMC$ thì $EF//IK$ và $\frac{EF}{IK}=\frac{CE}{CI}=\frac{2}{3}\Rightarrow EF=\frac{2}{3}IK=\frac {1}{3}ma$.

