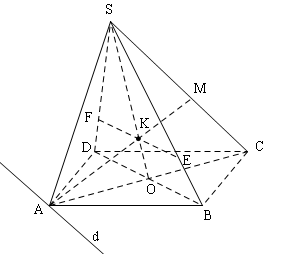
Đề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình chữ nhật, có cạnh $AB=12cm,AD=5cm$.Mặt phẳng $(P)$ đi qua $A$ và một điểm $M$ thuộc cạnh $SC$ và song song với đường chéo $BD$$a.$ Chứng minh rằng khi $M$ di chuyển trên $SC$ thì mặt phẳng $(P)$ luôn đi qua một đường thẳng cố định.$b.$ Dựng giao tuyến của mặt phẳng $(P)$ với mặt phẳng $(SBD)$$c.$ Gọi các giao điểm của $mp(P)$ với $SB,SD$ theo thứ tự là $E,F$.Tính độ dài đoạn thẳng $EF$ khi điểm $M$ là trung điểm của đoạn thẳng $SC$

Lời giải

$a.$ Mặt phẳng $(P)$ cắt mặt phẳng $(ABCD)$ thei giao tuyến là đường thẳng $d$ đi qua đỉnh $A$ và $d//DB$
$\Rightarrow  d$ là đường thẳng cố định mà mặt phẳng $(P)$ luôn đi qua.
$b.$ Giao tuyến của mặt phẳng $(P)$ với mặt phẳng $(SDB)$ là đường thẳng $EF//DB$.Do đó ta có cách dựng :
Gọi $O$ là giao điểm của $AC,DB$ trong mặt phẳng $(SAC)$, gọi $K$ là giao điểm của $SO,AM$
Dựng đường thẳng $EF$ đi qua $K$ và song song với $DB.EF=(P)\cap (SDB)$
$c.$ Ta có : $AB=12,AD=5\Rightarrow  DB=13 (cm)$
Khi $M$ là trung điểm của $SC$ thì $K$ là trọng tâm của $\Delta SAC$.Do $EF//DB$ nên :
$\frac{EF}{DB}=\frac{SK}{SO}=\frac{2}{3}   \Rightarrow  EF\approx 8,7 cm$