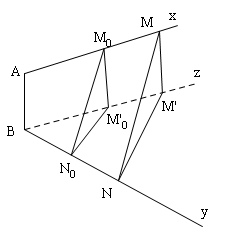
Đề bài: Cho hai nửa đường thẳng chéo nhau $Ax$ và $By$. Các điểm $M$ và $N$ lần lượt di động trên $Ax$ và $By$ sao cho $AM:BN=k$, trong đó $k$ là số khác $0$ cho trước. Chứng minh rằng $MN$ song song với một mặt phẳng cố định.

Lời giải

 Dựng tia $Bz$ song song với tia $Ax$. Trên các tia $Ax, By$ và $Bz$ lần lượt lấy các điểm cố định $M_0, N_0$ và $M’_0$ sao cho $\frac{AM_0}{BN_0}=k$ và $BM’_0=AM_0$.
Khi đó ta có: tứ giác $AM_0M’_0B$ là hình bình hành $M_0M’_0\parallel AB$ và $\frac{BM’_0}{BN_0}=k        (1)$.
Lấy điểm $M’\in$ tia $Bz$ sao cho $BM’=AM$. Khi đó ta có:
$MM’\parallel AB$ và $\frac{BM’}{BN}=k          (2)$
Từ $(1)$ và $(2)$ ta có: $MM’\parallel M_0M’_0, \frac{BM’}{BN}=\frac{BM’_0}{BN_0}$. Từ đây suy ra $NM’\parallel N_0M’_0$ và do đó mp$(MNM’)\parallel$ mp$(M_0N_0M’_0).$
Vậy $MN$ luôn song song với mặt phẳng cố định $(M_0N_0M’_0)$.