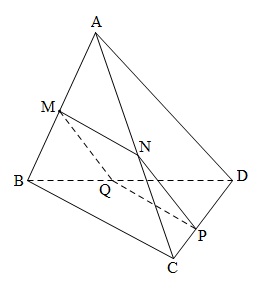
Đề bài: Cho tứ diện $ABCD$ có $\frac{AD}{BC}=k$. Lấy $M\in AB$ sao cho $\frac{AM}{AB}=n (0

Lời giải

Dễ thấy thiết diện là hình bình hành. Do $MN//BC$:
$\frac{MN}{BC}=\frac{AM}{AB}=n\Rightarrow MN=nBC$.
Có $BM=AB-AM=(1-n)AB\Rightarrow \frac {BM}{BA}=1-n$ 
Do $MQ//AD$  nên $\frac{MQ}{AD}=\frac{BM}{BA}=1-n\Rightarrow MQ=(1-n)AD$.
Muốn thiết diện là hình thoi, phải có $MN=MQ$ 
$\Leftrightarrow nBC=(1-n)AD\Leftrightarrow \frac{n}{1-n}=\frac{AD}{BC}=k\Rightarrow n=\frac{k}{1+k}$