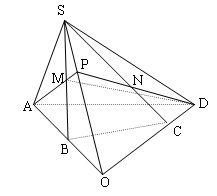
Đề bài: Trong mặt phẳng $\alpha$ cho tứ giác $ABCD$ có $AB$ và $CD$ không song song.$S$ là một điểm không thuộc $\alpha,M$ là điểm di động trên cạnh $SB$. Mặt phẳng $(ADM)$ cắt $SC$ tại $N$. Tìm tập hợp giao điểm của $AM,DN$

Lời giải

*Phần thuận
Ta có :
$AM\subset  (SAB)$- cố định
Mặt khác, vì $DN$ đi qua điểm cố định $D$ và cắt đường thẳng cố định $SC$ nên :
$DN\subset  (SCD)$- cố định
Giả sử $AB$ cắt $CD$ tại $O$ ta có ngay :
$(SAB)\cap (SCD)=SO$
Vậy tập hợp giao điểm $P$ của $AM$ và định nghĩa thuộc đường thẳng $SO$

*Giới hạn : Khi $M$ di chuyển trên cạnh $SB$ thì $P$ di chuyển trên đoạn $SO$

*Phần đảo
Gọi $P$ là điểm bất kì trên $SO$
– Nối $AP$ cắt $SB$ tại $M$
– Nối $DP$ cắt $SC$ tại $N,N$ là giao điểm của mặt phẳng $(ADM)$ với $SC$ và $P$ chính là giao điểm của $AM,DN$

Kết luận : Vậy tập hợp các điểm $P$ là đoạn $SO$.