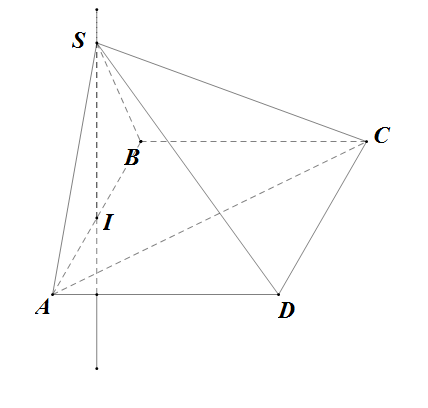
Đề bài: Trong mặt phẳng $(P)$ cho hình vuông $ABCD$ cạnh bằng $a$. Qua trung điểm $I$ của cạnh $AB$ dựng đường thẳng $d$ vuông góc với mặt phẳng $(ABCD)$. Trên $d$ lấy điểm $S$ sao cho $SI=\frac{a\sqrt{3}}{2}$.1) Tìm thể tích hình chóp $S.ACD$.2) Tìm khoảng cách từ $C$ đến $(SAD)$.

Lời giải

1) $V_{S.ACD}=\frac{1}{3}d(S,(ACD)).S_{ACD}=\frac{1}{3}\frac{a\sqrt{3}}{2}\frac{a^2}{2}=\frac{a^3\sqrt{3}}{12}$
2) $SA=\sqrt{SI^2+IA^2}=a$
$SD=\sqrt{SI^2+ID^2}=a\sqrt2$
$\Rightarrow \Delta SAD $vuông cân tại A
$\Rightarrow S_{SAD}=\frac{a^2}{2}\Rightarrow d(C,(SAD))=\frac{3V_{S.ACD}}{S_{SAD}}=\frac{a\sqrt{3}}{12}$
