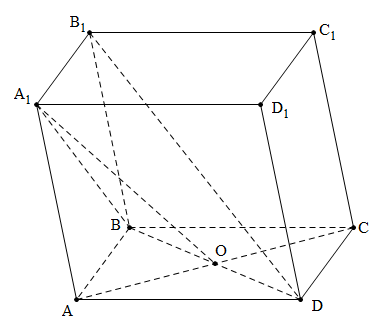
Đề bài: Cho hình lăng trụ $ABCD.A_1B_1C_1D_1$ có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{3}$. Hình chiếu vuông góc của $A_1$ lên mặt phẳng $(ABCD)$ trùng với giao điểm $O$ của hai đường chéo $AC,BD$ của đáy. Biết rằng hai mặt phẳng $(ADD_1A_1), (ABCD)$ tạo với nhau góc $60^0$. Tìm khoảng cách từ $ B_1$  đến mặt phẳng $(A_1BD)$.

Lời giải

Ta có $V_{B_1.A_1BD}=V_{D.A_1B_1B}=\frac{1}{2}V_{D.A_1B_1BA}   (1)$
Mặt khác ta có : $V_{D.A_1B_1BA}=\frac{1}{3}V_{DD_1C_1C.AA_1B_1B}   (2)$
 Ta lại có : $V_{DD_1C_1C.AA_1B_1B}=V_{ABCD.A_1B_1C_1D_1}=\frac{3a^3}{2}  (3)$
 từ $ (1),(2),(3)$ suy ra: $V_{B_1A_1BD}=\frac{a^3}{4}   (4)$
 Gọi $h$ là khoảng cách từ $B_1$ xuống mặt phẳng $(A_1BD)$, ta có:
   $V_{B_1A_1BD}=\frac{1}{3}h.S_{A_1BD}=\frac{1}{3}h.\frac{1}{2}BD.A_1O   (5)$
Thay $(4)$ vào $(5)$ ta có: $\frac{a^3}{4}=\frac{1}{6}h.2a.\frac{a\sqrt{3}}{2}$
(do $BD=\sqrt{AB^2+AD^2}=2a; A_1O= \frac{a\sqrt{3}}{2}$)
Từ đó suy ra $h=\frac{a\sqrt{3}}{2}$.