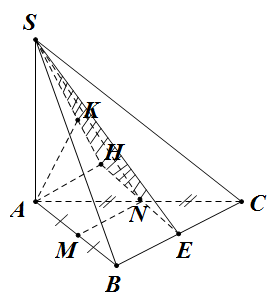
Đề bài: Cho hình chóp tam giác $S.ABC$ , đáy là tam giác vuông cân tại $B$, trong đó $AB=BC=2a$. Giả sử hai mặt phẳng $(SAB),(SAC)$ cùng vuông góc với mặt phẳng $(ABC)$. Gọi $M$ là trung điểm $AB$. Mặt phẳng qua $SM$ và song song với $BC$ cắt $ AC$ tại $N$.Biết rằng hai mặt phẳng $(SBC),(ABC)$ tạo với nhau góc $60^0$. Tìm khoảng cách giữa hai đường thẳng $AB,SN$ theo $a$.

Lời giải

Vẽ qua $N$ đường thẳng $NE// AB$.
Kẻ $AH \bot NE (H \in NE)$.
Rõ ràng $EB=EC=a$.
Ta có : $AB// (SHE)$ và $SN \in (SHE)$
$\Rightarrow d (AB,SN)=d(AB,(SHE))=d(A,(SHE))  (1)$
Ta có $AB \bot (SHA); SHE//AB\Rightarrow HE \bot (SAH)\Rightarrow (SHE)\bot (SAH)$
Vì $(SHE)\cap (SAH)=SH$,
Nên nếu kẻ $AK \bot SH\Rightarrow AK \bot (SHE)\Rightarrow d(A,(SHE))=AK (2)$

Trong tam giác vuông $SAH$ do $AK \bot SH \Rightarrow AK.SH=AH.SA$
$\Rightarrow AK= \frac{AH.SA}{SH}=\frac{a.2a\sqrt{3}}{\sqrt{a^2+12a^2}}=\frac{2a\sqrt{39}}{13}$.