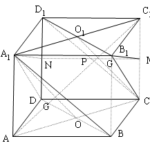
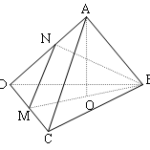
Đề bài: Cho hình hộp $ABCD.A_1B_1C_1D_1$$a.$ Chứng minh rằng $(BDA_1)//(B_1D_1C)$$b.$ Chứng minh đường chéo $AC_1$ đi qua các trọng tâm $G,G_1$ của $\Delta A_1BD$ và $\Delta CB_1D_1,G,G_1$ chia đoạn $AC_1$ làm $3$ phần bằng nhau.$c.$ Xác định thiết diện cắt bởi mặt phẳng $(A_1B_1G_1)$ với hình hộp đã cho. Thiết diện là hình gì ?$d.$ […]
Hình học không gian
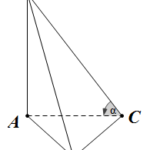
Đề bài: Hình chóp $S.ABC$ có đáy là tam giác vuông cân đỉnh $C$ và $SA$ vuông góc với đáy $(ABC)$. Giả sử $SC=a$. Hãy tìm góc giữa hai mặt phẳng $(SBC),(ABD)$ sao cho thể tích khối chóp là lớn nhất.
Đề bài: Hình chóp $S.ABC$ có đáy là tam giác vuông cân đỉnh $C$ và $SA$ vuông góc với đáy $(ABC)$. Giả sử $SC=a$. Hãy tìm góc giữa hai mặt phẳng $(SBC),(ABD)$ sao cho thể tích khối chóp là lớn nhất. Lời giải Ta thấy ngay $\widehat{SCA}=\alpha, SA=a\sin \alpha, AC=a\cos \alpha$.Suy ra: $V_{S.ABC}=\frac{1}{3}\frac{a^2\cos^2 \alpha}{2}.a\sin \alpha=\frac{a^3}{6}\cos^2 […]
Đề bài: Cho hình bình hành $ABCD$ nằm trong một mặt phẳng $(P)$ và một điểm $S$ ngoài mp $(P)$. Gọi $M$ là điểm thuộc đoạn thẳng $SA$ (không trùng $S, A$) và $N$ là điểm thuộc đoạn thẳng $SB$ (không trùng $S, B$), $O$ là giao điểm của hai đường thẳng $AC$ và $BD$.a) Tìm giao điểm của mp$(CMN)$ với đường thẳng $SO$.b) Xác định giao tuyến của mp$(SAD)$ và mp$(CMN)$
Đề bài: Cho hình bình hành $ABCD$ nằm trong một mặt phẳng $(P)$ và một điểm $S$ ngoài mp $(P)$. Gọi $M$ là điểm thuộc đoạn thẳng $SA$ (không trùng $S, A$) và $N$ là điểm thuộc đoạn thẳng $SB$ (không trùng $S, B$), $O$ là giao điểm của hai đường thẳng $AC$ và $BD$.a) […]
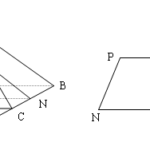
Đề bài: Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh $7a$, cạnh $SC$ vuông góc với mặt phẳng $(ABC)$ và $SC=7a$. Tìm khoảng cách giữa hai đường thẳng $SA$ và $BC$.
Đề bài: Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh $7a$, cạnh $SC$ vuông góc với mặt phẳng $(ABC)$ và $SC=7a$. Tìm khoảng cách giữa hai đường thẳng $SA$ và $BC$. Lời giải Trong (ABC) dựng hình bình hành ADBCTrong (ADC) dựng CH$\bot$ADTrong (SCH) dựng CK$\bot$SHAD$\bot$CH; AD$\bot$SC$\Rightarrow $AD$\bot$ (SCH) $\Rightarrow$ […]
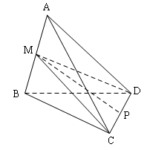
Đề bài: Cho tứ diện đều $ABCD$ cạnh bằng $a$. Gọi $O$ là tâm đường tròn ngoại tiếp $\Delta BCD$$a.$ Chứng minh rằng $AO\bot CD$$b.$ Gọi $M$ là trung điểm của $CD$. Tính góc giữa $AC,BM$
Đề bài: Cho tứ diện đều $ABCD$ cạnh bằng $a$. Gọi $O$ là tâm đường tròn ngoại tiếp $\Delta BCD$$a.$ Chứng minh rằng $AO\bot CD$$b.$ Gọi $M$ là trung điểm của $CD$. Tính góc giữa $AC,BM$ Lời giải $a.$ Ta có ngay kết luận $AO\bot CD$ vì $A.BCD$ là hình chóp tam giác đều$b.$ Gọi […]
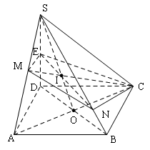
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình vuông $ABCD$ cạnh bằng $a$, mặt bên $(SAD)$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy $ABCD$. Gọi $M,N, P$ lần lượt là trung điểm của $SB,SC,CD$. Tìm thể tích tứ diện $CMNP$.
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình vuông $ABCD$ cạnh bằng $a$, mặt bên $(SAD)$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy $ABCD$. Gọi $M,N, P$ lần lượt là trung điểm của $SB,SC,CD$. Tìm thể tích tứ diện $CMNP$. Lời giải Cần giải chi tiết ( […]
Đề bài: Cho hình hộp $ABCD.A'B'C'D'$.Hãy phân tích các véctơ $\overrightarrow {AC};\overrightarrow {A'C};\overrightarrow {BD'} $ theo các véctơ $\overrightarrow {AB} ,\overrightarrow {AD} $ và $\overrightarrow {AA'} $
Đề bài: Cho hình hộp $ABCD.A'B'C'D'$.Hãy phân tích các véctơ $\overrightarrow {AC};\overrightarrow {A'C};\overrightarrow {BD'} $ theo các véctơ $\overrightarrow {AB} ,\overrightarrow {AD} $ và $\overrightarrow {AA'} $ Lời giải Cần giải chi tiếtĐáp số :$\overrightarrow {AC’}=\overrightarrow {AB}+\overrightarrow {AD}+\overrightarrow {AA’} $$\overrightarrow {AC’}=\overrightarrow {AB} +\overrightarrow {AD}-\overrightarrow {AA’} $$\overrightarrow {BD’}=-\overrightarrow {AB} +\overrightarrow {AD}+\overrightarrow {AA’} $$\overrightarrow {B’D}=-\overrightarrow {AB} +\overrightarrow […]
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật. Lấy $M, N$ lần lượt trên các cạnh $SB, SD$ sao cho: $\frac{{SB}}{{BM}} = \frac{{SN}}{{DN}} = 2$$1$. Mặt phẳng $(AMN)$ cắt cạnh $SC$ tại $P$. Tính tỉ số: $\frac{{SP}}{{CP}}$$2$. Tính thể tích hình chóp $S.AMPN$ theo thể tích $V$ của hình chóp $SABCD.$
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật. Lấy $M, N$ lần lượt trên các cạnh $SB, SD$ sao cho: $\frac{{SB}}{{BM}} = \frac{{SN}}{{DN}} = 2$$1$. Mặt phẳng $(AMN)$ cắt cạnh $SC$ tại $P$. Tính tỉ số: $\frac{{SP}}{{CP}}$$2$. Tính thể tích hình chóp $S.AMPN$ theo thể tích $V$ của hình chóp […]
Đề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình thang, đáy lớn $AB=3a,AD=CD=a$. Mặt bên $(SAB) $ là tam giác cân đỉnh $S$ với $SA=2a,\alpha$ là mặt phẳng di động song song với $(SAB)$ cắt các cạnh $AD,BC,SC,SD$ theo thứ tự tại $M,N,P,Q$$a.$ Chứng minh $MNPQ$ là hình thang cân$b.$ Đặt $x=AM$ với $0
Đề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình thang, đáy lớn $AB=3a,AD=CD=a$. Mặt bên $(SAB) $ là tam giác cân đỉnh $S$ với $SA=2a,\alpha$ là mặt phẳng di động song song với $(SAB)$ cắt các cạnh $AD,BC,SC,SD$ theo thứ tự tại $M,N,P,Q$$a.$ Chứng minh $MNPQ$ là hình thang cân$b.$ Đặt $x=AM$ với $0 […]
Đề bài: Cho tứ diện $ABCD$$a.$ Chứng minh hệ thức$\overrightarrow {AC}+\overrightarrow {BD}=\overrightarrow {AD}+\overrightarrow {BC} $$b) M$ là trung điểm của $AB;P$ là trung điểm của $CD.$Chứng minh hệ thức :$\overrightarrow {MP}=\frac{1}{4} (\overrightarrow {AC}+\overrightarrow {AD}+\overrightarrow {BC}+\overrightarrow {BD} )$
Đề bài: Cho tứ diện $ABCD$$a.$ Chứng minh hệ thức$\overrightarrow {AC}+\overrightarrow {BD}=\overrightarrow {AD}+\overrightarrow {BC} $$b) M$ là trung điểm của $AB;P$ là trung điểm của $CD.$Chứng minh hệ thức :$\overrightarrow {MP}=\frac{1}{4} (\overrightarrow {AC}+\overrightarrow {AD}+\overrightarrow {BC}+\overrightarrow {BD} )$ Lời giải $a.$ Ta có : $\overrightarrow {AC}+\overrightarrow {BD}=\overrightarrow {AD}+\overrightarrow {DC}+\overrightarrow {BC}+\overrightarrow {CD} $Kết hợp với $\overrightarrow {DC}+\overrightarrow […]