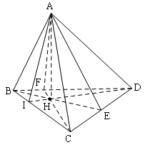
Đề bài: Cho tam giác $ABC$. Mặt phẳng song song với đường thẳng $BC$ cắt cạnh $AB$ tại $P$ và $AC$ tại $Q$. Điểm $P$ chia cạnh $AB$ theo tỉ số $3:5$ (bắt đầu từ điểm $A$). Tính độ dài đoạn $PQ$ nếu $BC=12cm$. Lời giải Giả sử có mặt phẳng $\alpha$ song song […]
Hình học không gian
Đề bài: Chứng minh rằng trong một tứ diện, nếu có hai cặp đối diện vuông góc thì cặp cạnh đối diện còn lại cũng vuông góc
Đề bài: Chứng minh rằng trong một tứ diện, nếu có hai cặp đối diện vuông góc thì cặp cạnh đối diện còn lại cũng vuông góc Lời giải Tứ diện $ABCD$ có $AB\bot CD$ và $AD\bot BC.$Ta cần chứng minh $AC\bot BD$.Từ $A$ kẻ $AE\bot CD$.Kết hợp với $AB\bot CD$ ta suy ra $CD\bot […]
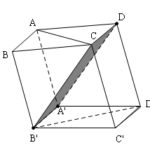
Đề bài: Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh cùng bằng nhau. Chứng minh rằng $AC\bot B'D'$. Nếu thêm giả thiết$\widehat{ABC}=\widehat{B'BA}=\widehat{B'BC}=60^0$Hãy chứng minh $A'B'CD$ là hình vuông.
Đề bài: Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh cùng bằng nhau. Chứng minh rằng $AC\bot B'D'$. Nếu thêm giả thiết$\widehat{ABC}=\widehat{B'BA}=\widehat{B'BC}=60^0$Hãy chứng minh $A'B'CD$ là hình vuông. Lời giải Ta có $AC\parallel A’C’$ và $A’B’C’D’$ là hình thoi nên $A’C’ \perp B’D’$. Mà $A’C’ \parallel AC$. Do đó $AC \perp B’D’$.Bây giờ, nếu […]
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là nửa lục giác đều nội tiếp đường tròn đường kính $AB=2a,SA=a\sqrt{3} $ và vuông góc với mặt phẳng $(ABCD)$$a.$ Tính góc giữa hai mặt phẳng $(SAD)$ và $(SBC)$$b.$ Tính góc giữa hai mặt phẳng $(SBC)$ và $(SCD)$
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là nửa lục giác đều nội tiếp đường tròn đường kính $AB=2a,SA=a\sqrt{3} $ và vuông góc với mặt phẳng $(ABCD)$$a.$ Tính góc giữa hai mặt phẳng $(SAD)$ và $(SBC)$$b.$ Tính góc giữa hai mặt phẳng $(SBC)$ và $(SCD)$ Lời giải $a.$ Ta có thể lựa chọn […]
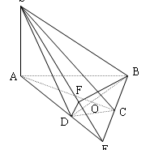
Đề bài: Cho tứ diện $OABC$ có $OA, OB, OC$ đôi một vuông góc $AC=2OB, BC=2OA$. Vẽ $OM\bot AC$ tại $M; ON\bot BC$ tại $N$a) Chứng minh $MN\bot OC$b) Tính $cos\widehat{MON}$ c) $D$ là trung điểm $AB$. chứng minh $\frac{tan^4\widehat{OCD}}{tan^4\widehat{OCA}}+\frac{MN}{AB} =1$
Đề bài: Cho tứ diện $OABC$ có $OA, OB, OC$ đôi một vuông góc $AC=2OB, BC=2OA$. Vẽ $OM\bot AC$ tại $M; ON\bot BC$ tại $N$a) Chứng minh $MN\bot OC$b) Tính $cos\widehat{MON}$ c) $D$ là trung điểm $AB$. chứng minh $\frac{tan^4\widehat{OCD}}{tan^4\widehat{OCA}}+\frac{MN}{AB} =1$ Lời giải Ta có: $\left\{ \begin{array}{l} OA^2+OC^2=AC^2\\ OB^2+OC^2=BC^2 \end{array} \right. $$\Rightarrow 4OB^2-OA^2=4OA^2-OB^2\Rightarrow OA=OB$Đặt $OA=a=OB\Rightarrow […]
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình thoi $ABCD$ cạnh bằng $a; SA=SB=SC=a$a. Chứng minh mặt phẳng $(ABCD)$ vuông góc với mặt phẳng $(SBD)$.b. Chứng minh $SBD$ là tam giác vuông tại $S$
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình thoi $ABCD$ cạnh bằng $a; SA=SB=SC=a$a. Chứng minh mặt phẳng $(ABCD)$ vuông góc với mặt phẳng $(SBD)$.b. Chứng minh $SBD$ là tam giác vuông tại $S$ Lời giải cần giải chi tiết.
Đề bài: Cho ba véctơ $\overrightarrow {v_1},\overrightarrow {v_2},\overrightarrow {v_3} $ sao cho vectơ $\overrightarrow {v_2} $ vuông góc với véctơ $(\overrightarrow {v_3}-\overrightarrow {v_1} )$ và véctơ $\overrightarrow {v_3} $ vuông góc với véctơ $(\overrightarrow {v_1}-\overrightarrow {v_2} )$.Chứng minh rằng véctơ $\overrightarrow {v_1} $ vuông góc với véctơ $(\overrightarrow {v_2}-\overrightarrow {v_3} )$
Đề bài: Cho ba véctơ $\overrightarrow {v_1},\overrightarrow {v_2},\overrightarrow {v_3} $ sao cho vectơ $\overrightarrow {v_2} $ vuông góc với véctơ $(\overrightarrow {v_3}-\overrightarrow {v_1} )$ và véctơ $\overrightarrow {v_3} $ vuông góc với véctơ $(\overrightarrow {v_1}-\overrightarrow {v_2} )$.Chứng minh rằng véctơ $\overrightarrow {v_1} $ vuông góc với véctơ $(\overrightarrow {v_2}-\overrightarrow {v_3} )$ Lời giải Ta có […]
Đề bài: Cho lăng trụ tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân với cạnh huyên $AB=a\sqrt{2}$. mặt phẳng $(AA'B)$ vuông góc với mặt phẳng $(ABC)$. Giả sử $AA'=a\sqrt{3}$, góc $\widehat{A'AB}$ nhọn và mặt phẳng $(A'AC)$ tạo với mặt phẳng $ABC)$ góc $60^0$. Tìm thể tích lăng trụ.
Đề bài: Cho lăng trụ tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân với cạnh huyên $AB=a\sqrt{2}$. mặt phẳng $(AA'B)$ vuông góc với mặt phẳng $(ABC)$. Giả sử $AA'=a\sqrt{3}$, góc $\widehat{A'AB}$ nhọn và mặt phẳng $(A'AC)$ tạo với mặt phẳng $ABC)$ góc $60^0$. Tìm thể tích lăng trụ. Lời giải Cần giải […]
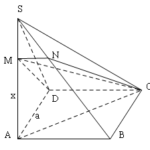
Đề bài: Cho chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,SA\bot (ABCD);SA=a$. Mặt phẳng $(P)$ đi qua $CD$ cắt $SA,SB$ lần lượt tại $M,N$. Đặt $AM=x$. Tứ giác $MNCD$ là hình gì ? Tính diện tích tứ giác đó theo $a,x$
Đề bài: Cho chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,SA\bot (ABCD);SA=a$. Mặt phẳng $(P)$ đi qua $CD$ cắt $SA,SB$ lần lượt tại $M,N$. Đặt $AM=x$. Tứ giác $MNCD$ là hình gì ? Tính diện tích tứ giác đó theo $a,x$ Lời giải Ta có : $DC//AB\Rightarrow DC//(SAB)$$\Rightarrow mp(MDC)\cap mp(SAB)=MN//AB$.Lại có $MN\bot (SAD)$.Suy […]
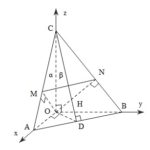
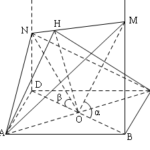
Đề bài: Cho hình vuông $ABCD$ tâm $O$, cạnh $a.$.Qua hai đỉnh $B,D$ ta kẻ hai tia $Bx,Dy$ cùng chiều và cùng vuông góc với $mp(ABCD)$.Một điểm $M$ thuộc $Bx$ và một điểm $N$ thuộc $Dy$ thỏa mãn hệ thức.$BM.DN=\frac{a^2}{2} $Đặt $\alpha =\widehat{BOM} $ và $\beta =\widehat{DON} $$a.$ Chứng minh hệ thức $\tan \alpha .\tan \beta =1$$b.$ Chứng minh $MN\bot AC$$c.$ Chứng minh $(ACM)\bot (CAN)$$d.$ Chứng minh $(AMN)\bot (CMN)$$e.$ Gọi $H$ là hình chiếu vuông góc của $O$ trên $MN$.Chứng minh : $AH\bot HC$
Đề bài: Cho hình vuông $ABCD$ tâm $O$, cạnh $a.$.Qua hai đỉnh $B,D$ ta kẻ hai tia $Bx,Dy$ cùng chiều và cùng vuông góc với $mp(ABCD)$.Một điểm $M$ thuộc $Bx$ và một điểm $N$ thuộc $Dy$ thỏa mãn hệ thức.$BM.DN=\frac{a^2}{2} $Đặt $\alpha =\widehat{BOM} $ và $\beta =\widehat{DON} $$a.$ Chứng minh hệ thức $\tan \alpha .\tan […]