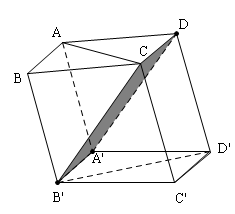
Đề bài: Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh cùng bằng nhau. Chứng minh rằng $AC\bot B'D'$. Nếu thêm giả thiết$\widehat{ABC}=\widehat{B'BA}=\widehat{B'BC}=60^0$Hãy chứng minh $A'B'CD$ là hình vuông.

Lời giải

Ta có $AC\parallel A’C’$ và $A’B’C’D’$ là hình thoi nên $A’C’ \perp B’D’$. Mà $A’C’ \parallel AC$. Do đó $AC \perp B’D’$.
Bây giờ, nếu thêm giả thiết $\widehat{ABC}=\widehat{B’BA}=\widehat{B’BC}=60^0$, ta có $A’B’CD$ là hình bình hành và $B’C=a=CD$ nên $A’B’CD$ là hình thoi. Ta lại có
$\overrightarrow{CB’}.\overrightarrow{CD}=(\overrightarrow{CB}+\overrightarrow{BB’}).\overrightarrow{BA}      $
$=\overrightarrow{CB}.\overrightarrow{BA}+\overrightarrow{BB’}.\overrightarrow{BA}=-\frac{a^2}{2}+\frac{a^2}{2}=0.      $
Vậy $CB’$ vuông góc $CD$, do đó $A’B’CD$ là hình vuông.