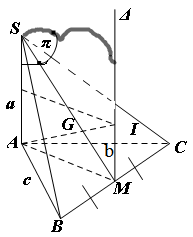
Đề bài: Cho hình chóp $S.ABC$ trong đó có đáy là tam giác vuông tại $A$. Giả sử $SA$ vuông góc với đáy. Biết $AB=c, AC=b, SA=a$. a) Xác định tâm $I$ và bán kính $R$ của hình cầu ngoại tiếp hình chóp $S.ABC$.b) Gọi $G$ là trọng tâm tam giác $SBC$. Chứng minh $A,G,I$ thẳng hàng.

Lời giải

a)Gọi $M$ là trung điểm của $BC$.
Do $\widehat{BAC}=90^0$ nên ta có: $MA=MB=MC$.
Qua $M$ dựng đường thẳng $\Delta $ vuông góc với $(ABC)$ (tức là $\Delta // SA$).

Trong mặt phẳng $(\pi)$ xác định bởi $SA$ và $\Delta$, ta dựng đường trung trực của $SA$. Đường này cắt $\Delta$ tại $I$.Khi đó:
$I$ chính là tâm hình cầu ngoại tiếp hình chóp $SABC$.
Ta có: $R=IA=\sqrt{IM^2+AM^2}=\sqrt{\frac{1}{4}SA^2+\frac{1}{4}BC^2}= \frac{1}{2}\sqrt{a^2+b^2+c^2}$.
b)Mặt phẳng $(\pi ): AI\cap SM=G$. Theo định lí Talet ta có:  $\frac{SG}{GM}=\frac{SA}{IM}=2$.
Vậy $G$ là trọng tâm tam giác $SBC$. Nói khác đi $A,G,I$ thẳng hàng $\Rightarrow $ đpcm.