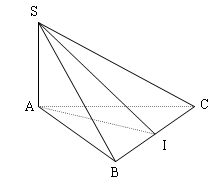
Đề bài: Cho hình chóp $S.ABC$ có $SA=a$ và vuông góc với mặt phẳng $(ABC),SB=2a,SC=a\sqrt{2} ,\widehat{SBC}=90^0$$a.$ Tính góc $\varphi$ giữa hai mặt phẳng $(ABC)$ và $(SBC)$$b.$ Tính diện tích $\Delta ABC$

Lời giải

$a.$ Hạ $SI\bot BC$ tại $I$ suy ra :
$AI\bot BC$ định lí ba đường vuông góc
Suy ra góc giữa hai mặt phẳng $(ABC),(SBC)$ là $\widehat{SIA}=\varphi $
Trong $\Delta SBC$ vuông tại $S$ ta có :
$\frac{1}{SI^2} =\frac{1}{SB^2}+\frac{1}{SC^2} =\frac{1}{4a^2}+\frac{1}{2a^2}=\frac{3}{4a^2} \Rightarrow SI=\frac{2a\sqrt{3} }{3} $
Trong $\Delta SAI$ vuông tại $A$ ta có : $\sin\varphi =\frac{SA}{SI}=\frac{a}{\frac{2a\sqrt{3} }{3} } =\frac{\sqrt{3} }{2} \Rightarrow \varphi =60^0$
$b.$ Ta có :
$S_{\Delta ABC}=S_{\Delta SBC}.cos \varphi =\frac{1}{2} SB.SC.cos60^0=\frac{1}{2} .2a.a\sqrt{2} .\frac{1}{2} =\frac{a^2\sqrt{2} }{2} $
