
Lời giải

$a.$ Ta có thể lựa chọn một trong hai cách trình bày sau :
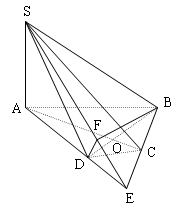
Cách $1:$ (Dựng góc dựa trên giao tuyến) : Giả sử :
$AD\cap BD$ vì $ABCD$ là nủa lục giác đều
$SA\bot BD$ giả thiết
suy ra :
$BD\bot (SAD)\Rightarrow BD\bot SE$
Hạ $DF\bot SE$ tại $F$ suy ra :
$(BDF)\bot SE$
Như vậy ta được một góc giữa hai mặt phẳng $(SAD)$ và $(SBC)$ là $\widehat{BFD} $
Vì $\Delta ABE$ đều nên $AE=AB=2a$
Vì $\Delta CDE$ đều nên $DE=CD=a$
Trong $\Delta SAE$ vuông tại $S$ ta có :
$SE^2=SA^2+AE^2=(a\sqrt{3} )^2+(2a)^2=7a^2\Rightarrow SE=a\sqrt{7} $
Hai tam giác vuông $SAE,DFE$ có chung góc $\widehat{E} $ nên chúng đồng dạng, suy ra :
$\frac{DF}{SA}=\frac{DE}{SE}\Rightarrow DF=\frac{SA.DE}{SE}=\frac{a\sqrt{3}.a }{a\sqrt{7} } =\frac{a\sqrt{21} }{7} $
Trong $\Delta ABD$ vuông tại $A$ ta có :$BD=ABsin\widehat{BAD}=2a.cos60^0=a\sqrt{3} $
Trong $\Delta BDF$ vuông tại $D$ ta có :
$tan\widehat{BFD}=\frac{BD}{DE}=\frac{a\sqrt{3} }{\frac{a\sqrt{21} }{7} } =\sqrt{7}\Rightarrow \widehat{BFD} $ nhọn
Vậy ta được $tan((SAD),(SBC))=\sqrt{7} $
Cách $2:$ Nhận xét rằng :
$AD\bot BD$ vì $ABCD$ là nửa lục giác đều
$SA\bot BD$ giả thiết
suy ra $BD\bot (SAD) (1)$
Trong $(SAC)$ hạ $AJ\bot SC$ tại $J$ ta có
$BC\bot AC$ vì $ABCD$ là nửa lục giác đều nội tiếp
$BC\bot SA$ giả thiết
suy ra $BC\bot (SAC)\Rightarrow BC\bot AJ\Rightarrow AJ\bot (SBC) (2)$
Trong $(SAc)$ hạ $OK\bot SC$ tại $K$ suy ra $OK//AJ (3)$
Từ $(1),(2),(3)$ suy ra :
$((SAD),(SBC))=(BD,AJ)=(BD,OK)=\widehat{KOB} $
Trong nửa lục giác đều $ABCD$ ta có:
$OC=\frac{2}{3}.\frac{a\sqrt{3} }{2}=\frac{a\sqrt{3} }{3} $
$OB=\frac{a\sqrt{3} }{2} +\frac{1}{3} .\frac{a\sqrt{3} }{2} =\frac{2a\sqrt{3} }{2} $
Trong $\Delta SAC$ vuông tại $S$ ta có :
$SC^2=SA^2+AC^2=SA^2+(AB^2-BC^2)$
$=(a\sqrt{3} )^2+(4a^2-a^2)=6a^2\Rightarrow SC=a\sqrt{6} $
Hai tam giác vuông $SAC,OKC$ có chung góc nhon $\widehat{C} $ nên chúng đồng dạng, suy ra :
$\frac{OK}{SA}=\frac{OC}{SC}\Rightarrow OK=\frac{SA.OC}{SC}=\frac{a\sqrt{3}.\frac{a\sqrt{3} }{3} }{a\sqrt{6} } =\frac{a\sqrt{6} }{6} $
Trong $\Delta KOB$ vuông tại $K$ ta có:
$cos\widehat{KOB}=\frac{OK}{OB}=\frac{\frac{a\sqrt{6} }{6} }{\frac{2a\sqrt{3} }{3} } =\frac{\sqrt{2} }{4} $
Vậy ta được $cos((SAD),(SBC))=\frac{\sqrt{2} }{4} $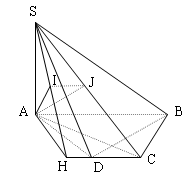
$b.$ Trong $(SAC)$ hạ $AJ\bot SC$ tại $J$ ta có :
$BC\bot AC$ vì $ABCD$ là nửa lục giác đều nội tiếp
$BC\bot SA$ giả thiết
suy ra :
$BC\bot (SAC)\Rightarrow BC\bot AJ\Rightarrow AJ\bot (SBC) (4)$
Hạ $AH\bot CD$ tại $H$ suy ra :
$\begin{cases} CD\bot AH\\CD\bot SA\end{cases} \Rightarrow CD\bot (SAH)$
$\Rightarrow (SCD)\bot (SAH)$ và $(SCD)\bot (SAH)=SH$
Hạ $AI\bot SH$ tại $I$ suy ra $AI\bot (SCD) (5)$
Từ $(4),(5)$ suy ra
$((SCD),(SBC))=\widehat{IAJ} $
Trong $\Delta SAH$ vuông tại $A$ ta có :
$AH=\frac{a\sqrt{3} }{2} $
$\frac{1}{AI^2}=\frac{1}{SA^2}+\frac{1}{AH^2} =\frac{1}{(a\sqrt{3} )^2}+\frac{1}{(\frac{a\sqrt{3} }{2} )^2} =\frac{5}{3a^2} \Rightarrow AI=\frac{a\sqrt{15} }{5} $
Trong $\Delta SAC$ vuông tại $A$ ta có :
$AC=SA=a\sqrt{3}\Rightarrow AJ=\frac{1}{2} SC=\frac{SA\sqrt{2} }{2} =\frac{a\sqrt{6} }{2} $
Trong $\Delta AIJ$ vuông tại $I$ ta có :
$cos\widehat{IAJ}=\frac{AI}{AJ}=\frac{\frac{a\sqrt{15} }{5} }{\frac{a\sqrt{6} }{2} } =\frac{\sqrt{10} }{5} $
Vậy ta được $cos((SCD),(SBC))=\frac{\sqrt{10} }{5} $
