Đề bài: Cho tứ diện $OABC$ có $OA, OB, OC$ đôi một vuông góc $AC=2OB, BC=2OA$. Vẽ $OM\bot AC$ tại $M;  ON\bot BC$ tại $N$a) Chứng minh $MN\bot OC$b) Tính $cos\widehat{MON}$ c) $D$ là trung điểm $AB$. chứng minh $\frac{tan^4\widehat{OCD}}{tan^4\widehat{OCA}}+\frac{MN}{AB}  =1$

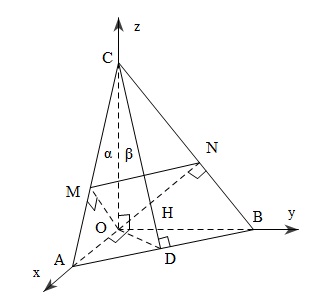
Lời giải

Ta có: $\left\{ \begin{array}{l} OA^2+OC^2=AC^2\\ OB^2+OC^2=BC^2 \end{array} \right. $
$\Rightarrow  4OB^2-OA^2=4OA^2-OB^2\Rightarrow  OA=OB$
Đặt $OA=a=OB\Rightarrow  OC=a\sqrt{3} $

a) $\overrightarrow{AC}=(-a;0;a\sqrt{3} )=-a(1;0;-\sqrt{3} ) $
$\Rightarrow  $ phương trình tham số $AC:\left\{ \begin{array}{l} x=a+t\\ y=0\\z=-\sqrt{3}t  \end{array} \right. $
$\Rightarrow  M(a+t;0;-\sqrt{3} t)$
$OM\bot AC\Rightarrow  \overrightarrow{OM}.\overrightarrow{AC} =0\Leftrightarrow  a+t+0+3t=0 $
$\Leftrightarrow  t=-\frac{a}{4}\Rightarrow  M(\frac{3a}{4};0;\frac{a\sqrt{3} }{4}  ) $
$\overrightarrow{BC}=(0;-a;a\sqrt{3} )=-a(0;1;-\sqrt{3} ) $
Suy ra phương trình $BC:\left\{ \begin{array}{l} x=0\\ y=a+t\\z=-\sqrt{3} t \end{array} \right. \Rightarrow  N(0;a+t;-\sqrt{3}t )$
$ON\bot BC\Rightarrow  \overrightarrow{ON}.\overrightarrow{BC}=0\Leftrightarrow  a+t+3t=0  $
$t=-\frac{a}{4}\Rightarrow  N(0;\frac{3a}{4};\frac{a\sqrt{3} }{4}  ) \Rightarrow  \overrightarrow{MN}.\overrightarrow{OC}=(-\frac{3a}{4};\frac{3a}{4};0  ) (0;0;a\sqrt{3} ) =0$
Vậy $MN\bot OC$

b) $\widehat{MON}=\frac{\overrightarrow{OM}.\overrightarrow{ON}  }{OM.ON} =\frac{\frac{3a^2}{16} }{\frac{12a^2}{16} } =\frac{1}{4} $

c) Đặt $\beta =\widehat{OCD};   \alpha =\widehat{OCA}$
$OC\bot (OAB)\Rightarrow  OC\bot OD$
$OD=\frac{1}{2}AB=\frac{a\sqrt{2} }{2}  $
$\Rightarrow  tan \beta =\frac{OD}{OC};  tan \alpha =\frac{OA}{OC} \Rightarrow  \frac{tan^4 \beta }{tan^4\alpha }=(\frac{OD}{OA})^2=\frac{1}{4}    $
$\frac{MN}{AB}=\frac{\frac{3a\sqrt{2} }{4} }{a\sqrt{2} }  \frac{3}{4} \Rightarrow  \frac{tan^4\widehat{OCD}}{tan^4\widehat{OCA}}+\frac{MN}{AB}=1  $