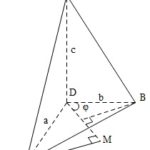
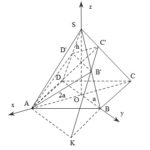
Đề bài: Cho tứ diện $ABCD$, trong đó góc tam diện đỉnh $D$ là tam diện vuông. Giả sử $DA=a, DB=b, DC=c$. Chứng minh rằng với mỗi điểm $M$ nằm trên một cạnh của $\triangle ABC$ thì: $S=d(A,DM)+d(B,DM)+d(C,DM) \leq \sqrt{2(a^2+b^2+c^2)}$Khi nào xảy ra dấu bằng, ở đây $d(A,DM)$ là khoảng cách từ $A$ đến […]
Hình học không gian
Đề bài: Cho hai mặt phẳng $(P)$ và $(Q)$ vuông góc với nhau, gọi $d$ là giao tuyến của chúng. Cho $2$ điểm $A\in (Q), B\in (P)$ thỏa mãn khoảng cách từ $B$ đến $(Q)$ bằng khoảng cách từ $A$ đến $(P)$. Chứng minh góc tạo bởi $AB$ với mặt phẳng $(P)$ và mặt phẳng $(Q)$ bằng nhau.
Đề bài: Cho hai mặt phẳng $(P)$ và $(Q)$ vuông góc với nhau, gọi $d$ là giao tuyến của chúng. Cho $2$ điểm $A\in (Q), B\in (P)$ thỏa mãn khoảng cách từ $B$ đến $(Q)$ bằng khoảng cách từ $A$ đến $(P)$. Chứng minh góc tạo bởi $AB$ với mặt phẳng $(P)$ và mặt phẳng […]
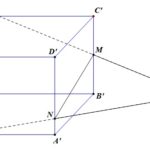
Đề bài: Cho hình lập phương $ABCD.A’B’C’D’$. Dựng mặt phẳng chứa đường chéo $AC$ của hình vuông $ABCD$ và đi qua trung điểm $M$ của cạnh $B’C’$. Mặt phẳng đó chia hình lập phương thành hai phần. Tính tỉ số thể tích của $2$ hình đó.
Đề bài: Cho hình lập phương $ABCD.A’B’C’D’$. Dựng mặt phẳng chứa đường chéo $AC$ của hình vuông $ABCD$ và đi qua trung điểm $M$ của cạnh $B’C’$. Mặt phẳng đó chia hình lập phương thành hai phần. Tính tỉ số thể tích của $2$ hình đó. Lời giải Mặt phẳng $(P)$ cắt mặt phẳng $A’B’C’D’$ […]
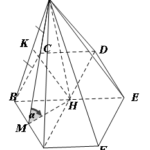
Đề bài: Cho hình chóp lục giác đều $S.ABCDEF$ cạnh đáy bằng $a$, góc của mặt bên và đáy là $\alpha$. Tìm bán kính hình cầu ngoại tiếp, hình cầu nội tiếp hình chóp.
Đề bài: Cho hình chóp lục giác đều $S.ABCDEF$ cạnh đáy bằng $a$, góc của mặt bên và đáy là $\alpha$. Tìm bán kính hình cầu ngoại tiếp, hình cầu nội tiếp hình chóp. Lời giải Gọi $H$ là tâm của đáy. Do $S.ABCDEF$ là chóp đều nên mọi điểm trên đường cao $SH$ đều […]
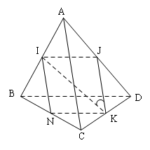
Đề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$
Đề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$ Lời giải cần giải […]
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$. Gọi $M$ và $N$ lần lượt là trung điểm của các cạnh $AB$ và $AD, H$ là giao điểm của $CN$ và $DM.$ Biết $SH$ vuông góc với mặt phẳng $ABCD$ và $SH$ =$a \sqrt{ 3}.$ Tính thể tích khối chóp $S.CDNM$ và khoảng cách giữa hai đường thẳng $DM$ và $SC$ theo $a.$
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$. Gọi $M$ và $N$ lần lượt là trung điểm của các cạnh $AB$ và $AD, H$ là giao điểm của $CN$ và $DM.$ Biết $SH$ vuông góc với mặt phẳng $ABCD$ và $SH$ =$a \sqrt{ 3}.$ Tính thể tích khối chóp […]
Đề bài: Hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi với các đường chéo $AC=4a, BD=2a$, chúng cắt nhau tại $O$. Đường cao hình chóp $SO=h$. Mặt phẳng $(\alpha )$ qua $A$, vuông góc với $SC$ và cắt $SB, SC, SD$ lần lượt tại $B',C',D'$a) Xác định $h$ để $\Delta B'C'D'$ đềub) Tính bán kính $r$ của mặt cầu nội tiếp hình chóp theo $a$ và $h$
Đề bài: Hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi với các đường chéo $AC=4a, BD=2a$, chúng cắt nhau tại $O$. Đường cao hình chóp $SO=h$. Mặt phẳng $(\alpha )$ qua $A$, vuông góc với $SC$ và cắt $SB, SC, SD$ lần lượt tại $B',C',D'$a) Xác định $h$ để $\Delta B'C'D'$ đềub) Tính bán […]
Đề bài: Cho lăng trụ tam giác $ABC.A'B'C'$.Hãy xác định thiết diện của lăng trụ với một mặt phẳng $(P)$ đi qua các điểm $M,N,P$ thuộc ba mặt bên
Đề bài: Cho lăng trụ tam giác $ABC.A'B'C'$.Hãy xác định thiết diện của lăng trụ với một mặt phẳng $(P)$ đi qua các điểm $M,N,P$ thuộc ba mặt bên Lời giải Giả sử ta cần dựng thiết diện của lăng trụ $ABC.A’B’C’$ khi cắt bởi mặt phẳng $(P)$ đi qua ba điểm$M\in (ABB’A’)$$N\in (BCC’B’)$$P\in (CAA’C’)$Qua […]
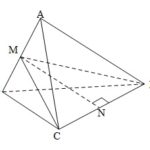
Đề bài: Cho tứ diện đều $ABCD$ cạnh $a$. Gọi $M, N$ theo thứ tự là trung điểm các cạnh $AB, CD$. Tìm độ dài đoạn $MN$
Đề bài: Cho tứ diện đều $ABCD$ cạnh $a$. Gọi $M, N$ theo thứ tự là trung điểm các cạnh $AB, CD$. Tìm độ dài đoạn $MN$ Lời giải Vì $ABCD$ là tứ diện đều cạnh $a$ nên các đường trung tuyến $CM=DM=\frac{a\sqrt{3}}{2}\Rightarrow \Delta CMD$ là tam giác cân đỉnh $M\Rightarrow MN$ vuông góc với […]
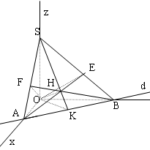
Đề bài: Trong mặt phẳng $\alpha$ cho góc vuông $xOy,d$ là đường thẳng cố định trong $\alpha,d$ cắt $Ox,Oy$ lần lượt tại $A,B$.Gọi $Oz$ là tia vuông góc với $\alpha,S$ là một điểm trên $Oz$.Gọi $AE,BF$ là đường cao của $\Delta SAB$$a.$ Cho góc $xOy$ cố định,$S$ di động trên tia $Oz$.Tìm tập hợp các điểm $E,F$$b.$ Cho $d$ cố định, góc $xOy$ xoay quanh $O$.Chứng minh rằng trực tâm của $\Delta SAB$ cố định.Tìm tập hợp các điểm $E,F$
Đề bài: Trong mặt phẳng $\alpha$ cho góc vuông $xOy,d$ là đường thẳng cố định trong $\alpha,d$ cắt $Ox,Oy$ lần lượt tại $A,B$.Gọi $Oz$ là tia vuông góc với $\alpha,S$ là một điểm trên $Oz$.Gọi $AE,BF$ là đường cao của $\Delta SAB$$a.$ Cho góc $xOy$ cố định,$S$ di động trên tia $Oz$.Tìm tập hợp các […]