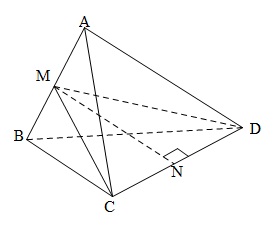
Đề bài: Cho tứ diện đều $ABCD$ cạnh $a$. Gọi $M, N$ theo thứ tự là trung điểm các cạnh $AB, CD$. Tìm độ dài đoạn $MN$

Lời giải

Vì $ABCD$ là tứ diện đều cạnh $a$ nên các đường trung tuyến $CM=DM=\frac{a\sqrt{3}}{2}\Rightarrow \Delta CMD$ là tam giác cân đỉnh $M\Rightarrow MN$ vuông góc với $CD$.  Áp dụng định lý Pitago vào tam giác vuông $MND$ 
Ta có: 
 $MN^2=MD^2-ND^2=(\frac{a\sqrt{3}}{2})^2-(\frac{a}{2})^2=\frac{a^2}{2}\Rightarrow MN=\frac{a\sqrt{2}}{2}$.