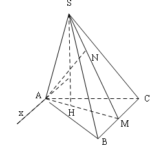
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, canh bên $SA=a$; hình chiếu vuông góc của đỉnh $S$ trên mặt phẳng $(ABCD)$ là điểm $H$ thuộc đoạn $AC, AH =$ $\frac{ AC}{4}$. Gọi $CM$ là đường cao của tam giác $SAC$. Chúng minh $M$ là trung điểm của $SA $và tính thể tích khối tứ diện $SMBC$ theo $a$. Lời giải $AC= AB\sqrt2=a \sqrt{ … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, canh bên $SA=a$; hình chiếu vuông góc của đỉnh $S$ trên mặt phẳng $(ABCD)$ là điểm $H$ thuộc đoạn $AC, AH =$ $\frac{ AC}{4}$. Gọi $CM$ là đường cao của tam giác $SAC$. Chúng minh $M$ là trung điểm của $SA $và tính thể tích khối tứ diện $SMBC$ theo $a$.
Hình học không gian
Đề bài: Cho hai mặt phẳng $(P),(Q)$ giao nhau theo giao tuyến $\Delta $.Trong mặt phẳng $(P)$ lấy một điểm $A$ không thuộc $\Delta $ và trong mặt phẳng $(Q)$ lấy một điểm $B$ không thuộc $\Delta $.Chứng minh đường thẳng $AB$ và đường thẳng $\Delta $ là hai đường thẳng chéo nhau
Đề bài: Cho hai mặt phẳng $(P),(Q)$ giao nhau theo giao tuyến $\Delta $.Trong mặt phẳng $(P)$ lấy một điểm $A$ không thuộc $\Delta $ và trong mặt phẳng $(Q)$ lấy một điểm $B$ không thuộc $\Delta $.Chứng minh đường thẳng $AB$ và đường thẳng $\Delta $ là hai đường thẳng chéo nhau Lời giải Chứng minh bằng phản chứng.Nếu $\Delta ,AB$ không chéo nhau thì dẫn đến kết luận … [Đọc thêm...] vềĐề bài: Cho hai mặt phẳng $(P),(Q)$ giao nhau theo giao tuyến $\Delta $.Trong mặt phẳng $(P)$ lấy một điểm $A$ không thuộc $\Delta $ và trong mặt phẳng $(Q)$ lấy một điểm $B$ không thuộc $\Delta $.Chứng minh đường thẳng $AB$ và đường thẳng $\Delta $ là hai đường thẳng chéo nhau
Đề bài: Cho hình chóp đều $S.ABC$ có cạnh đáy bằng $a$$a)$ Hãy dựng mặt phẳng $(P)$ đi qua $A$ song song với đường thẳng $BC$ và vuông góc với mặt phẳng $(SBC)$$b)$ Giả sử góc giữa mặt phẳng $(P)$ và mặt đáy là $\alpha$.Gọi $M$ là trung điểm cạnh $BC$.Tính $SM$ theo $a$ và $\alpha$
Đề bài: Cho hình chóp đều $S.ABC$ có cạnh đáy bằng $a$$a)$ Hãy dựng mặt phẳng $(P)$ đi qua $A$ song song với đường thẳng $BC$ và vuông góc với mặt phẳng $(SBC)$$b)$ Giả sử góc giữa mặt phẳng $(P)$ và mặt đáy là $\alpha$.Gọi $M$ là trung điểm cạnh $BC$.Tính $SM$ theo $a$ và $\alpha$ Lời giải a) Theo đinh nghĩa của hình chóp đều, dễ thấy $AM,SM$ cung vuông góc với … [Đọc thêm...] vềĐề bài: Cho hình chóp đều $S.ABC$ có cạnh đáy bằng $a$$a)$ Hãy dựng mặt phẳng $(P)$ đi qua $A$ song song với đường thẳng $BC$ và vuông góc với mặt phẳng $(SBC)$$b)$ Giả sử góc giữa mặt phẳng $(P)$ và mặt đáy là $\alpha$.Gọi $M$ là trung điểm cạnh $BC$.Tính $SM$ theo $a$ và $\alpha$
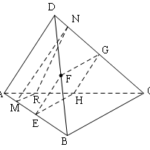
Đề bài: Cho tứ diện $ABCD$.Một điểm $M$ thuộc cạnh $AB$ và một điểm $N$ thuộc cạnh $CD$ sao cho : $\frac{AM}{AB}=\frac{DN}{DC}=k $$a.$ Chứng minh ba đường thẳng $BC,MN,AD$ luôn song song với một mặt phẳng cố định khi $k$ thay đổi$b.$ Một điểm $P$ trên $BD$ và một điểm $Q$ trên $AC$ sao cho :$\frac{PD}{BD}=\frac{AQ}{AC}=k' $Chứng minh rằng hai đường thẳng $MN,PQ$ cắt nhau khi và chỉ khi $k=k'$
Đề bài: Cho tứ diện $ABCD$.Một điểm $M$ thuộc cạnh $AB$ và một điểm $N$ thuộc cạnh $CD$ sao cho : $\frac{AM}{AB}=\frac{DN}{DC}=k $$a.$ Chứng minh ba đường thẳng $BC,MN,AD$ luôn song song với một mặt phẳng cố định khi $k$ thay đổi$b.$ Một điểm $P$ trên $BD$ và một điểm $Q$ trên $AC$ sao cho :$\frac{PD}{BD}=\frac{AQ}{AC}=k' $Chứng minh rằng hai đường thẳng $MN,PQ$ cắt … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD$.Một điểm $M$ thuộc cạnh $AB$ và một điểm $N$ thuộc cạnh $CD$ sao cho : $\frac{AM}{AB}=\frac{DN}{DC}=k $$a.$ Chứng minh ba đường thẳng $BC,MN,AD$ luôn song song với một mặt phẳng cố định khi $k$ thay đổi$b.$ Một điểm $P$ trên $BD$ và một điểm $Q$ trên $AC$ sao cho :$\frac{PD}{BD}=\frac{AQ}{AC}=k' $Chứng minh rằng hai đường thẳng $MN,PQ$ cắt nhau khi và chỉ khi $k=k'$
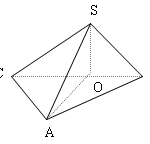
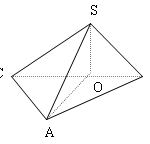
Đề bài: Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông tại $A,BC=a,SA=SB=SC=\frac{a\sqrt{3} }{2} $$a.$ Tính khoảng cách từ $S$ tới mặt phẳng $(ABC)$$b.$ Tính góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$
Đề bài: Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông tại $A,BC=a,SA=SB=SC=\frac{a\sqrt{3} }{2} $$a.$ Tính khoảng cách từ $S$ tới mặt phẳng $(ABC)$$b.$ Tính góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$ Lời giải $a.$ Gọi $O$ là trung điểm của $BC$ suy ra $O$ là tâm đường tròn ngoại tiếp $\Delta ABC$Ngoài ra theo giả thiết ta có : $SA=SB=SC$ nên $SO$ là trục … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông tại $A,BC=a,SA=SB=SC=\frac{a\sqrt{3} }{2} $$a.$ Tính khoảng cách từ $S$ tới mặt phẳng $(ABC)$$b.$ Tính góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$
Đề bài: Trong tất cả các hình nón ngoại tiếp hình trụ chiều cao $h$, bán kính $R$ hãy xác định hình nón có thể tích nhỏ nhất.
Đề bài: Trong tất cả các hình nón ngoại tiếp hình trụ chiều cao $h$, bán kính $R$ hãy xác định hình nón có thể tích nhỏ nhất. Lời giải GiảiĐặt $x$ là độ dài bán kính đáy của hình nón ngoại tiếp hình trụ $(x>R)$ ta có thể tích hình nón là $V=\frac{\pi hx^3}{3(x-R)}$Áp dụng bất đẳng thức Cô-si ta có: $3\sqrt[3]{\frac{x-R}{x}.\frac{R}{2x}.\frac{R}{2x}} \leq … [Đọc thêm...] vềĐề bài: Trong tất cả các hình nón ngoại tiếp hình trụ chiều cao $h$, bán kính $R$ hãy xác định hình nón có thể tích nhỏ nhất.
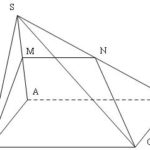
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, cạnh $SA$ vuông góc với đáy. Độ dài các cạnh $AB = a; AD = b; SA = 2a$. Gọi $M$ là trung điểm của đoạn $SA.$Mặt phẳng ($MBC$) cắt hình chóp theo thiết diện gì? Tính diện tích thiết diện đó
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, cạnh $SA$ vuông góc với đáy. Độ dài các cạnh $AB = a; AD = b; SA = 2a$. Gọi $M$ là trung điểm của đoạn $SA.$Mặt phẳng ($MBC$) cắt hình chóp theo thiết diện gì? Tính diện tích thiết diện đó Lời giải Giao tuyến của mp $(MBC)$ và mp $(SAD)$ cắt $SD$ tại $N:MN//BC$ vì $AD//BC$$MB\bot BC$ vì $BC\bot … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, cạnh $SA$ vuông góc với đáy. Độ dài các cạnh $AB = a; AD = b; SA = 2a$. Gọi $M$ là trung điểm của đoạn $SA.$Mặt phẳng ($MBC$) cắt hình chóp theo thiết diện gì? Tính diện tích thiết diện đó
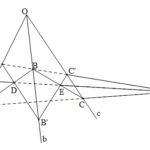
Đề bài: Cho ba tia $Oa, Ob, Oc$ không cùng nằm trên một mặt phẳng; trên tia $Oa$ lấy $2$ điểm $A, A'$; trên tia $Ob$ lấy $2$ điểm $B, B'$; trên tia $Oc$ lấy $2$ điểm $C, C'$ sao cho $AB$ cắt $A'B'$ tại $D$, $BC$ cắt $B'C'$ tại $E$; $CA$ cắt $C'A'$ tại $G$. Chứng minh $D, E ,G$ thẳng hàng.
Đề bài: Cho ba tia $Oa, Ob, Oc$ không cùng nằm trên một mặt phẳng; trên tia $Oa$ lấy $2$ điểm $A, A'$; trên tia $Ob$ lấy $2$ điểm $B, B'$; trên tia $Oc$ lấy $2$ điểm $C, C'$ sao cho $AB$ cắt $A'B'$ tại $D$, $BC$ cắt $B'C'$ tại $E$; $CA$ cắt $C'A'$ tại $G$. Chứng minh $D, E ,G$ thẳng hàng. Lời giải Ta thấy, muốn chứng minh … [Đọc thêm...] vềĐề bài: Cho ba tia $Oa, Ob, Oc$ không cùng nằm trên một mặt phẳng; trên tia $Oa$ lấy $2$ điểm $A, A'$; trên tia $Ob$ lấy $2$ điểm $B, B'$; trên tia $Oc$ lấy $2$ điểm $C, C'$ sao cho $AB$ cắt $A'B'$ tại $D$, $BC$ cắt $B'C'$ tại $E$; $CA$ cắt $C'A'$ tại $G$. Chứng minh $D, E ,G$ thẳng hàng.
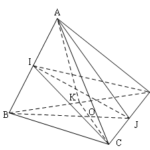
Đề bài: Cho tứ diện đều $ABCD$ có cạnh bằng $a.$Gọi $I,J,K$ lần lượt là trung điểm của $AB,CD,BD$$a.$ Chứng minh rằng $(ABJ)$ là mặt phẳng trung trực của $CD$, đồng thời mặt phẳng này tạo với hai mặt phẳng $(CAB),(DAB)$ hai góc bằng nhau.$b,$ Tính số đo của góc tạo bởi $mp(ACK)$ và $mp(ABJ)$
Đề bài: Cho tứ diện đều $ABCD$ có cạnh bằng $a.$Gọi $I,J,K$ lần lượt là trung điểm của $AB,CD,BD$$a.$ Chứng minh rằng $(ABJ)$ là mặt phẳng trung trực của $CD$, đồng thời mặt phẳng này tạo với hai mặt phẳng $(CAB),(DAB)$ hai góc bằng nhau.$b,$ Tính số đo của góc tạo bởi $mp(ACK)$ và $mp(ABJ)$ Lời giải $a.$ Các mặt của tứ diện là các tam giác đều, nên $AJ,BJ$ cùng … [Đọc thêm...] vềĐề bài: Cho tứ diện đều $ABCD$ có cạnh bằng $a.$Gọi $I,J,K$ lần lượt là trung điểm của $AB,CD,BD$$a.$ Chứng minh rằng $(ABJ)$ là mặt phẳng trung trực của $CD$, đồng thời mặt phẳng này tạo với hai mặt phẳng $(CAB),(DAB)$ hai góc bằng nhau.$b,$ Tính số đo của góc tạo bởi $mp(ACK)$ và $mp(ABJ)$
Đề bài: Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông tại $A,BC=a,SA=SB=SC=\frac{a\sqrt{3} }{2} $$a.$ Tính khoảng cách từ $S$ tới mặt phẳng $(ABC)$$b.$ Tính góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$
Đề bài: Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông tại $A,BC=a,SA=SB=SC=\frac{a\sqrt{3} }{2} $$a.$ Tính khoảng cách từ $S$ tới mặt phẳng $(ABC)$$b.$ Tính góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$ Lời giải $a.$ Gọi $O$ là trung điểm của $BC$ suy ra $O$ là tâm đường tròn ngoại tiếp $\Delta ABC$Ngoài ra theo giả thiết ta có : $SA=SB=SC$ nên $SO$ là trục … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông tại $A,BC=a,SA=SB=SC=\frac{a\sqrt{3} }{2} $$a.$ Tính khoảng cách từ $S$ tới mặt phẳng $(ABC)$$b.$ Tính góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$