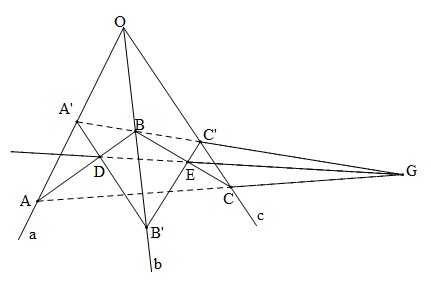
Đề bài: Cho ba tia $Oa, Ob, Oc$ không cùng nằm trên một mặt phẳng; trên tia $Oa$ lấy $2$ điểm $A, A'$; trên tia $Ob$ lấy $2$ điểm $B, B'$; trên tia $Oc$ lấy $2$ điểm $C, C'$ sao cho $AB$ cắt $A'B'$ tại $D$, $BC$ cắt $B'C'$ tại $E$; $CA$ cắt $C'A'$ tại $G$. Chứng minh $D, E ,G$ thẳng hàng.

Lời giải

Ta thấy, muốn chứng minh $D, E, G$ thẳng hàng ta phải chứng minh chúng thuộc giao tuyến của hai mặt phẳng phân biệt . Ta có $D\in AB$ và $AB\subset (ABC)\Rightarrow D\in mp (ABC). D\in A’B’$ mà $A’B’\subset (A’B’C’)$
$\Rightarrow D\in mp (A’B’C’)$  nên $D$ là điểm chung của hai mặt phẳng $(ABC)$ và $(A’B’C’)$. Cũng chứng minh tương tự hai điểm $E, G$ cùng là điểm chung của hai mp $(ABC)$ và $(A’B’C’)$. Vậy $D, E, G$ phải nằm trên giao tuyến của hai mặt phẳng $(ABC)$ và $(A’B’C’)$, nên chúng thẳng hàng.